Закон Ома в дифференциальной форме
Содержание
Обычно для расчётов электрического тока пользуются законом Ома для участка цепи: I=U/R, где I – ток в цепи, U – напряжение, R – суммарное сопротивление. Ток в этой цепи может протекать через различные участки из разных проводов. Поэтому для расчётов силы тока в определённом участке проводника лучше применить закон Ома в дифференциальной форме. Так как плотность тока Ī – векторная величина, то формула закона имеет вид: Ī = γĒ, где γ – удельная проводимость, обратная удельному сопротивлению γ=1/R, а Ē – напряжённость электрического поля. Может выражаться закон Ома также в интегральных формах.
Действие электродвижущих сил
Электродвижущая сила (ЭДС) является скалярной величиной, характеризующей работу не электрических сил, заставляющих производить разность потенциалов на выходе.
Используется ЭДС в генераторах, преобразующих какую либо работу А (джоуль) в электрическую. Для этого могут быть использованы такие виды энергии по их происхождению:
- Механическая индукционная. Вывод ЭДС возникает при пересечении проводником линий магнитного поля;
- Механическая пьезоэлектрическая. Возникновение ЭДС происходит при деформации некоторых веществ;
- Световая энергия. Здесь ЭДС появляется в полупроводниках при действии на них световых лучей;
- Термическая энергия. ЭДС образуется, когда контакты из разнородных проводников находятся под разными температурами;
- Химическая энергия. Возникновение ЭДС происходит вследствие химических реакций.
В зависимости от характера энергии и устройства генератора ЭДС может возникать как переменная, так и постоянная. Переменная может быть как синусоидальная (магнитные индукционные генераторы), так и импульсная (пьезозажигалки). Постоянную ЭДС преобразуют в основном из химической (элементы питания, аккумуляторы), световой (фотоэлементы) энергий и температуры (элементы Пельтье).
ЭДС образует на разноименных проводниках разность потенциалов. Если не соединять проводником клеммы, на которых имеется разность потенциалов, то тока в цепи не будет. Следовательно, никакой энергии не будет израсходовано. На клеммах будет оставаться разность потенциалов. Работу для поддержания этой разности совершать не надо.
Если к клеммам с разностью потенциалов подключить проводник с нагрузкой, то через него будет протекать электрический ток, выполняя работу в нагрузке. При этом разность потенциалов на клеммах будет стремиться к 0, что приведёт к падению тока до 0. Для поддержания разности потенциалов стабильной величиной необходимо, чтобы ЭДС получала энергию. Эта энергия затрачивает работу, равную той, которая совершается в нагрузке.
Движение тока по неоднородным проводникам
Разность потенциалов, вызванная ЭДС, будет производить напряжение на клеммах генератора. ЭДС – это скалярная величина. При подключении к клеммам проводника через него потечёт ток, плотность которого выражается, например, Ī. Это уже векторная величина. Если ток создан только разностью потенциалов на клеммах, то векторы потенциала и плотности тока будут совпадать. Такой проводник называют однородным. Закон Ома для однородного участка цепи:
I=U/R.
Неоднородный проводник, кроме сил, которые образованы разностями потенциалов, имеет сторонние силы. Для определения плотности тока Ī пользуются законом Ома в дифференциальной форме для неоднородных проводников:
Ī=γ(E+Ē₁+ Ē₂+ Ēn).
Векторы и каждый участок проводника складываются, E – напряжённость, созданная разностью потенциалов на клеммах проводника (скалярная величина). Ē₁, Ē₂, Ēn – векторные величины напряжённости первой, второй и энной сторонних сил.
Так как γ – удельная проводимость проводника, обратная сопротивлению, ϕ₁ – потенциал на 1-ой точке, ϕ₂ – потенциал на 2-ой точке, то закон Ома для неоднородного участка цепи от 1-ой до 2-ой точки будет записываться так:
Ī =(ϕ₁ – ϕ₂+ Ē)/R.
Для ознакомления металлы и их удельное сопротивление:
- Серебро – 1,6×10ˉ⁸Ом×м;
- Медь – 1,72×10ˉ⁸ Ом×м;
- Алюминий – 2,6×10ˉ⁸ Ом×м;
- Латунь – 3…7,0×10ˉ⁸ Ом×м;
- Бронза – 8,0×10ˉ⁸ Ом×м;
- Железо – 9,8×10ˉ⁸ Ом×м;
- Свинец – 2.0×10ˉ⁶Ом×м;
- Графит – 3…5,0×10ˉ⁵Ом×м.
Трактовка и пределы применимости закона Ома
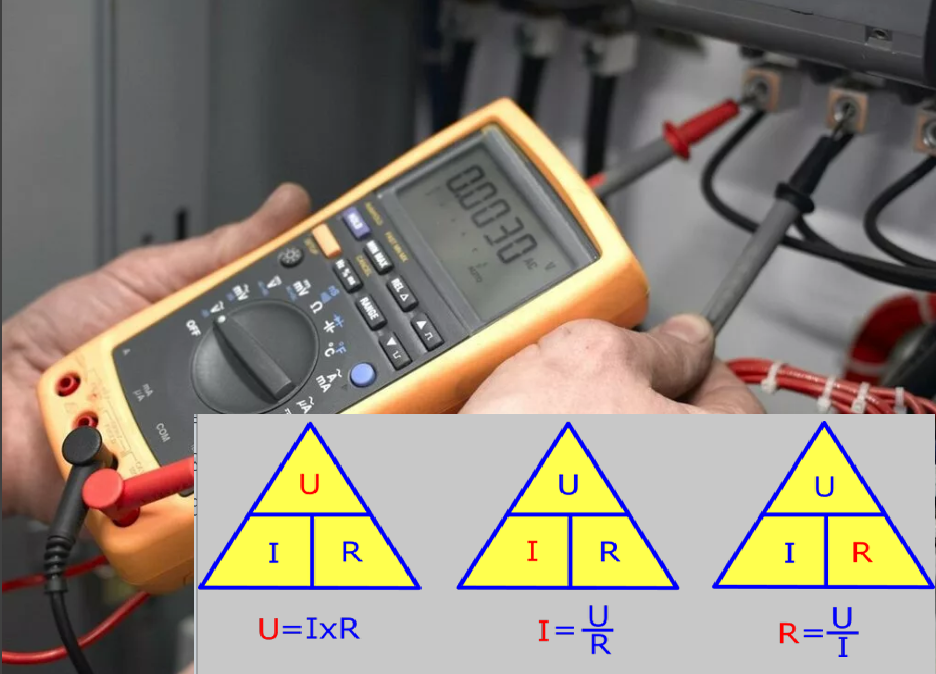
Если необходимо определить одну из величин: ток, напряжение или сопротивление для однородной цепи, то пользуются формулой, формулировка которой изображена на рисунке.
Для удобства решения тождества величины изображены в треугольнике. Теперь, пользуясь первой формулой, зная сопротивление цепи и ток, можно высчитать напряжение, которое действует на замкнутый контур. Зная напряжение и сопротивление цепи, можно определить ток по 2-ой формуле. По 3-ей формуле высчитывают сопротивление нагрузки, зная напряжение и ток.
Существуют исключения, когда закон Ома не соблюдается. Примеры:
- В переменных ЭДС, если нагрузка имеет индукционный или ёмкостный характер. При повышении частоты из-за инерционности носителей заряда вступают в силу законы электродинамики. Конденсаторы и катушки индуктивности в качестве сопротивления для переменного тока, колебательный контур.
- Для веществ, обладающих сверхпроводимостью при низких температурах. Датчики измерительных приборов высокой точности, сверхпроводящие соленоиды, сверхпроводящие кабели с током 5 000 А.
- При высоких температурах, когда проводник начинает проявлять нелинейную характеристику сопротивления. Вольфрамовая нить лампы накаливания, спирали нагревательных элементов.
- При высоких напряжениях, когда происходит пробой диэлектрика. Свечи зажигания карбюраторных двигателей, наконечники для защиты от тлеющего разряда высоковольтных ЛЭП.
- В наполненных газом люминесцентных и вакуумных лампах. Люминесцентные лампы, вакуумные индикаторы, индикаторы тлеющего разряда.
- В полупроводниковых приборах с p-n переходами и в нелинейных полупроводниках. Это светодиоды, стабилитроны, транзисторы, электронные приборы.
Материалы проводников, к которым применяется закон Ома, названы оммическими или линейными проводниками. Те, у которых сопротивление имеет функциональную зависимость от интенсивности тока, – нелинейными. Так могут вести себя металлы при крайне низких или высоких температурах.