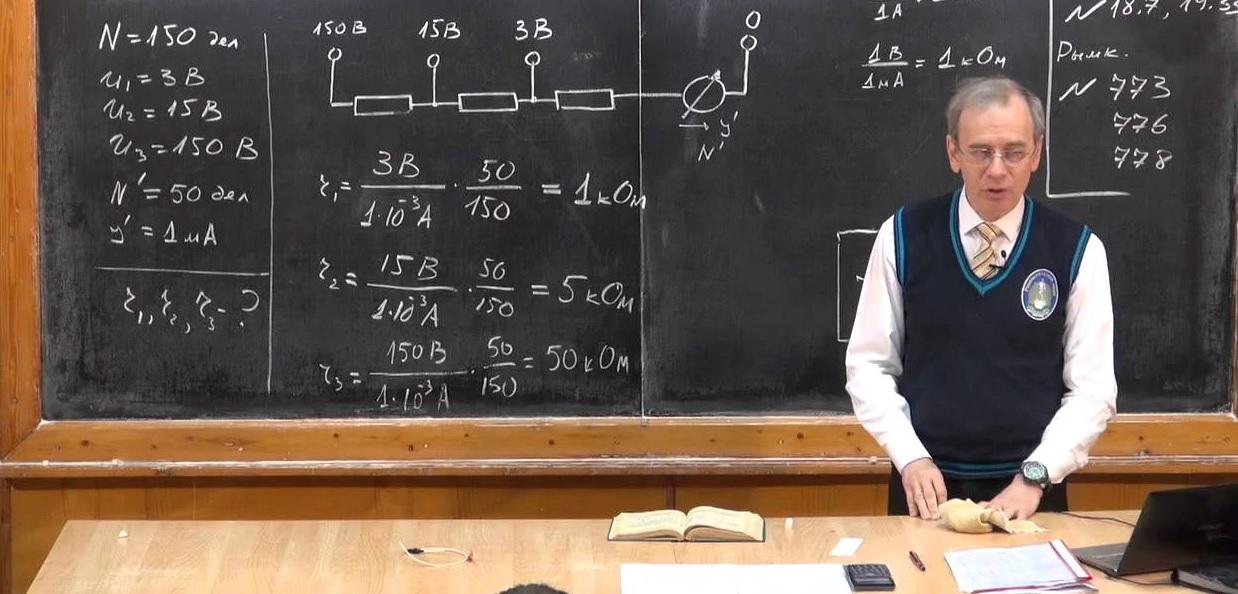Расчет электрических цепей
Содержание
Для вычисления рабочих параметров радиотехнических устройств и отдельных схем применяют специальные методики. После изучения соответствующих технологий результат можно узнать быстро, без сложных практических экспериментов. Корректный расчет электрических цепей пригодится на стадии проектирования и для выполнения ремонтных работ.
Задачи на расчет электрических цепей решают с применением типовых алгоритмов
Категории элементов и устройств электрической цепи
Для условного изображения определенной цепи применяют специальную схему. Кроме отдельных физических компонентов, она содержит сведения о направлении (силе) токов, уровнях напряжения и другую информацию. Качественная модель показывает реальные процессы с высокой точностью.
Компоненты электрической цепи:
- источник постоянного или переменного тока (Е) – аккумулятор или генератор, соответственно;
- пассивные элементы (R) – резисторы;
- компоненты с индуктивными (L) и емкостными (С) характеристиками;
- соединительные провода.
Типовые названия
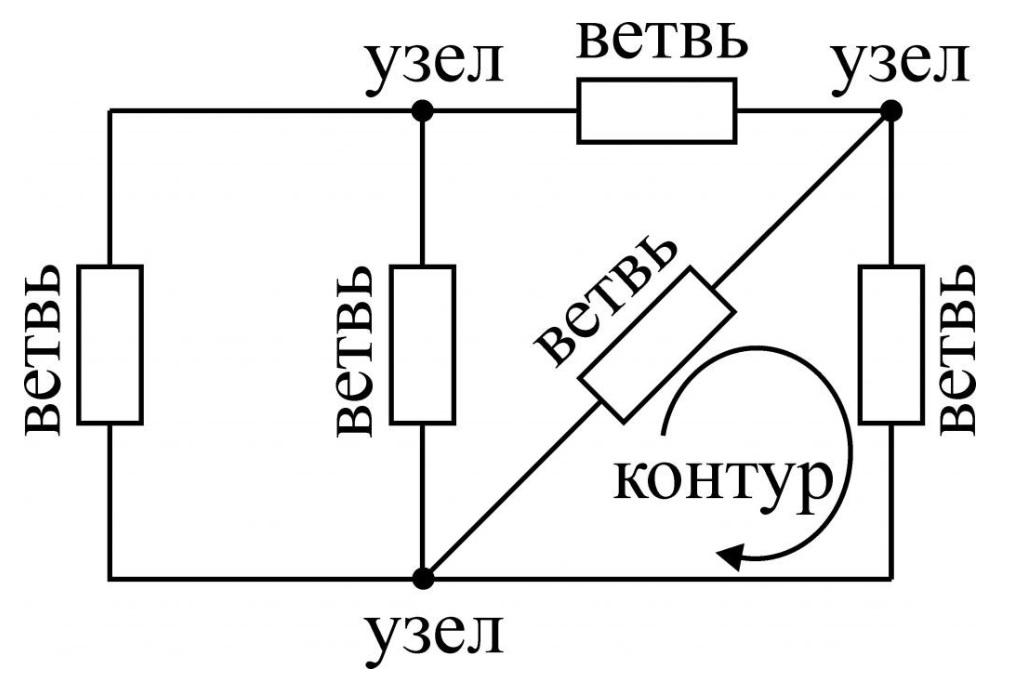
На рисунке обозначены:
- ветви – участки цепи с одним током;
- узлы – точки соединения нескольких ветвей;
- контур – замкнутый путь прохождения тока.
При решении практических задач выясняют, как узнать силу тока в отдельных ветвях. Полученные значения используют для анализа электрических параметров. В частности, можно определять падение напряжения на резисторе, мощность потребления подключенной нагрузки. При расчете цепей переменного тока приходится учитывать переходные энергетические процессы, влияние частоты.
Метод расчета по законам Ома и Кирхгофа
До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:
- последовательное – увеличивает общее сопротивление;
- параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.
Закон Ома для участка цепи
Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (< 1 мм), высокая плотность тока в соответствующем поперечном сечении быстро увеличит температуру вплоть до теплового разрушения материала с разрывом цепи. Этот пример демонстрирует функциональность обычного плавкого предохранителя.
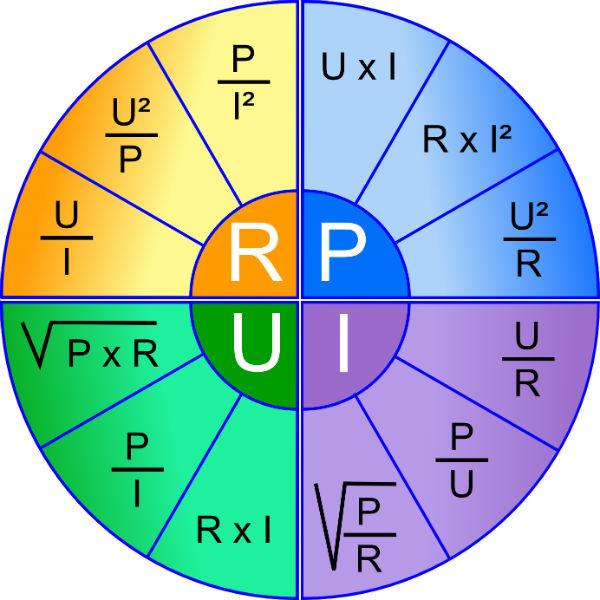
Подключив нагрузку, можно мультиметром проверить напряжение. Значение этого параметра остается неизменным. Если известно сопротивление (пример – R = 50 Ом), применение закона Ома (I = U/ R) поможет рассчитать ток:
I = 12/ 50 = 0,24 А.
По вычисленному значению с использованием формулы быстро определяется мощность:
P = I2 *R = U2/ R = 0,0576 * 50 = 2,88 Вт.
На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.
Закон Ома для полной цепи
Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:
I = U/ (Rэкв + Rвн).
Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.
Первый закон Кирхгофа
По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:
I1 + I2 + … + In = 0.
Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.
Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:
- входящие – положительные (+I);
- выходящие – отрицательные (-I).
Второй закон Кирхгофа
Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:
- UR1 = 10 V;
- UR1 = 2 V;
- Uакб = 12 V = UR1 + UR2 = 10 + 2;
- ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
- при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.
Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.
Метод преобразования электрической цепи
Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.
Расчет цепи с одним источником питания
Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:
Rэкв = R1 + R2 + … + Rn.
Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:
E = Ur1 + Ur2 + Urn.
Параллельное соединение резисторов, схемотехника и формулы для расчетов
В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.
Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:
- R1 = 10 Ом;
- R2 = 20 Ом;
- R3= 15 Ом;
- U = 12 V.
По следующему алгоритму будут определяться характеристики цепи:
- базовая формула для трех элементов:
Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.
- подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
- I = 12/ 4,615 ≈ 2,6 А;
- I1 = 12/ 10 = 1,2 А;
- I2 = 12/20 = 0,6 А;
- I3 = 12/15 = 0,8 А.
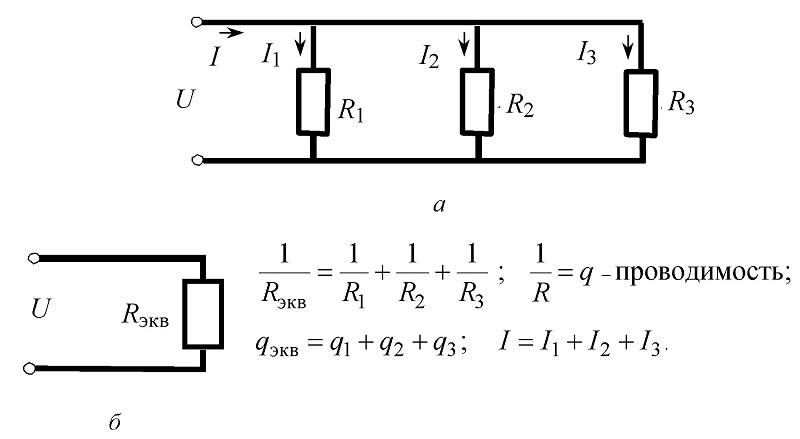
Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:
I = 1,2 + 0,6 + 0,8 = 2,6 А.
Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:
- частоты сигнала (f);
- индуктивности (L).
Вычисляют ХL по формуле:
ХL = 2π * f * L.
Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:
Хc = 1/ 2π * f * C.
Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.
Расчет разветвленной электрической цепи с несколькими источниками питания
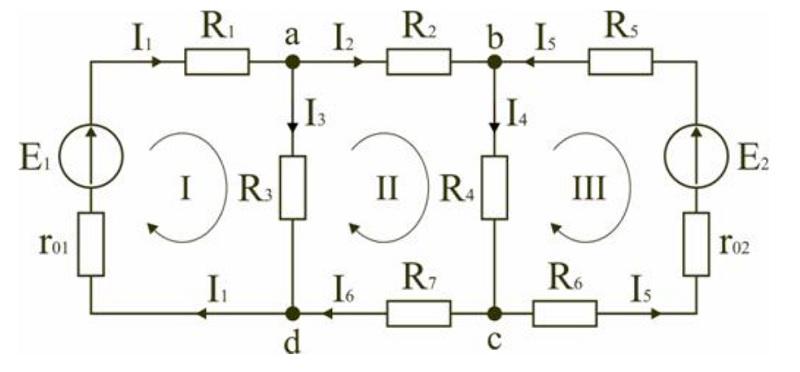
Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:
- обозначают компоненты и базовые параметры во всех контурах;
- составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
- в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
- проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.
Пояснительная схема к расчету с двумя источниками
Дополнительные методы расчета цепей
В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.
Метод узлового напряжения
Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.
Метод эквивалентного генератора
Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.
Графическое пояснение
В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.
