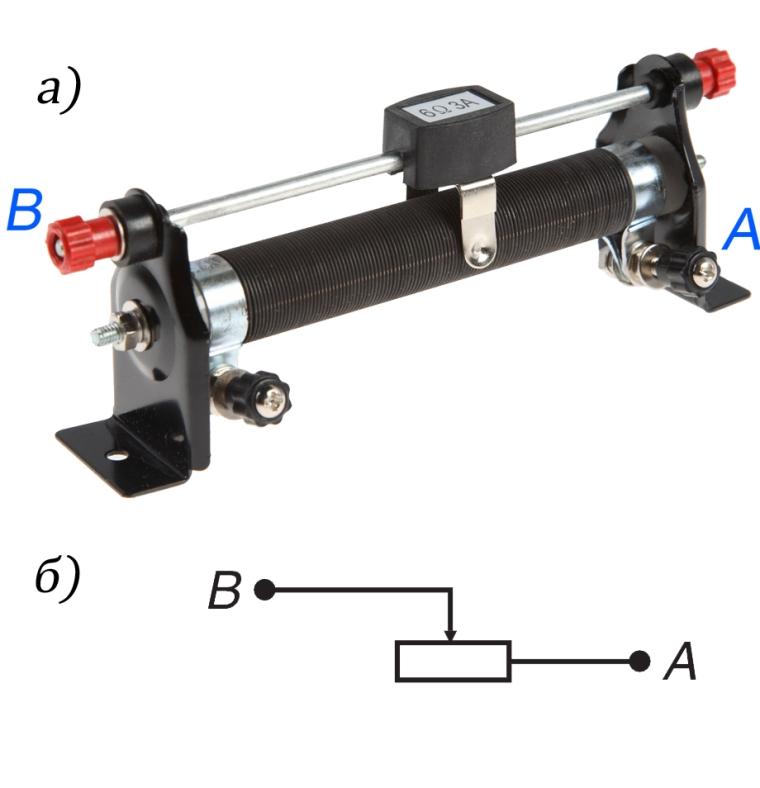
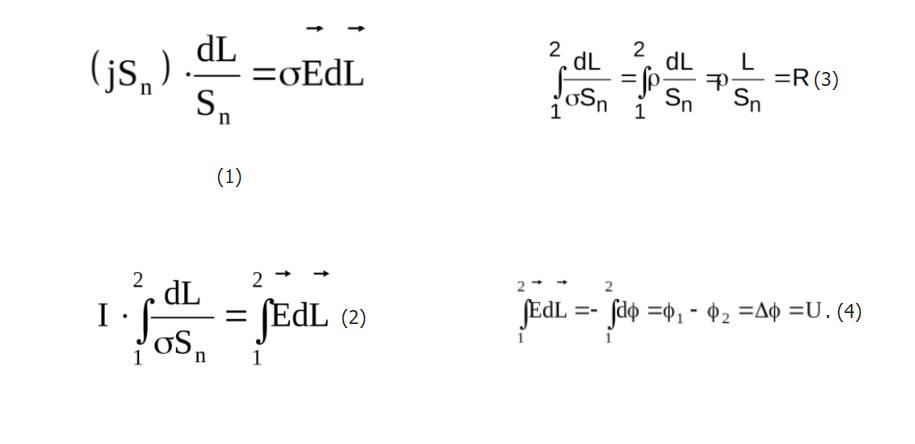Закон Ома для участка цепи
Содержание
Для теоретических расчетов и применения полученных результатов на практике оценивают силу тока, напряжения и сопротивление проводника. Взаимные зависимости базовых параметров определяет закон Ома для участка цепи. Созданные в начале 19 века формулы применяют для конструирования, проверки и модернизации электротехнических схем любого уровня сложности.
Закон Ома сформулирован в 1826 году
Формула закона Ома для однородного участка цепи
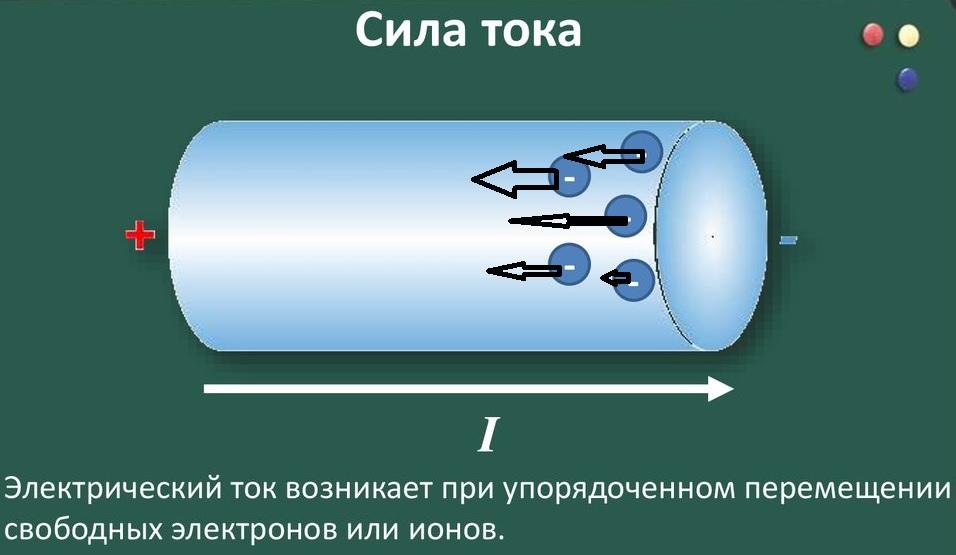
Для создания тока в проводнике нужно создать разницу потенциалов между определенными точками с применением источника питания. Этим действием активизируют перемещение заряженных частиц. Ток направляется в сторону меньшего потенциала, причем электроны будут перемещаться в обратном направлении.
Направление силы тока противоположно движению отрицательно заряженных частиц
Разную полярность можно отобразить соответствующими потенциалами ϕ1(+)>ϕ2(-). Вычитанием определенных величин получают значение напряжения (эдс, электродвижущую силу) на участке созданной цепи:
ϕ1- ϕ2 = U.
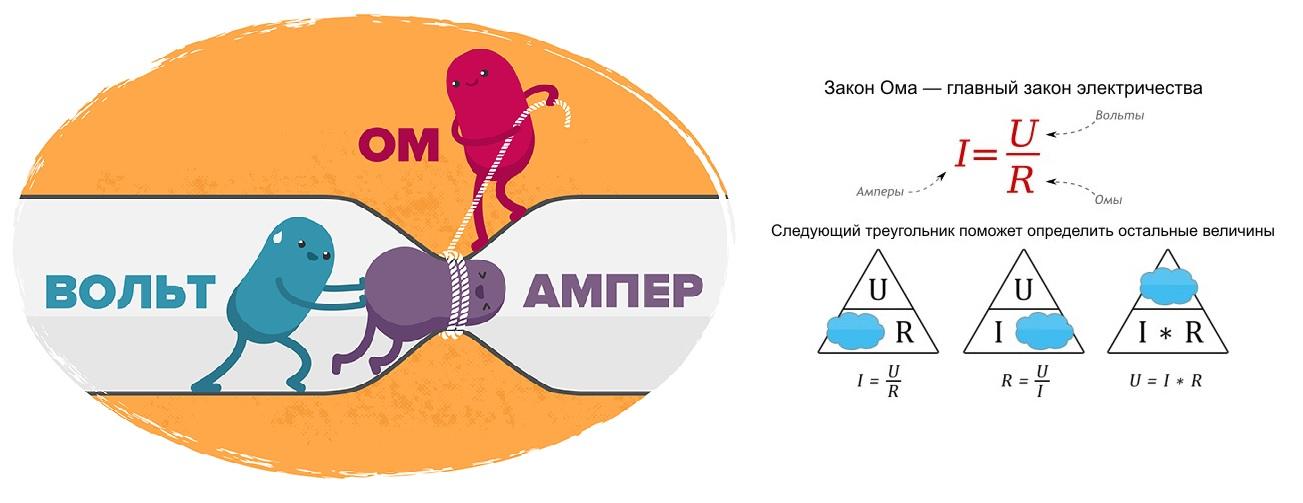
В ходе упомянутых практических экспериментов Георг Ом установил прямую зависимость силы тока (I) от увеличения разницы потенциалов. Одновременно было отмечено влияние материала проводника. Этот параметр – электрическое сопротивление (R), по мере увеличения препятствует прохождению тока. Итоговые зависимости выражаются известной формулой:
I = U/R.
«Магический» треугольник помогает запомнить алгоритмы типовых вычислений
На левой стороне рисунка наглядно изображены основные принципы рабочего процесса. Напряжение обеспечивает перемещение заряженных частиц. Сопротивление определяет условия для этого действия. Математическим преобразованием (правая сторона) можно получить формулы (треугольник), чтобы вычислять третий параметр по известным значениям двух других (i u r):
- R=U/I;
- U = I * R.
Отмеченное влияние проводника выражают через специальный коэффициент (p), которым обозначают удельное сопротивление. При рассмотрении контрольного образца следует учесть площадь поперечного сечения (S, в мм кв.) и длину (L, м). Итоговая формула для электрического сопротивления на основе перечисленных параметров:
R = p * (L/S).
Ее можно использовать при необходимости в комплексе с зависимостями закона Ома:
I = (U * S)/(p * L).
На основе рассмотренных процессов можно сформулировать энергетические потери, которые создает однородный участок цепи. На перемещение зарядов между двумя точками с разными потенциалами будут потрачена мощность:
P = U * I.
Прямо пропорциональный характер этого математического выражения подчеркивает соответствующую зависимость параметра от напряжения на участке цепи, тока. При необходимости в алгоритм вычислений добавляют электрическое сопротивление.
Закон Ома для неоднородного участка цепи
В реальных условиях для поддержания перемещения зарядов с определенной интенсивностью необходимо приложение сторонних сил, а не только кулоновских. Рассмотренный ниже пример демонстрирует участок замкнутой цепи, который называют неоднородным.
Описание закона
Формулировка этого принципа справедлива для любых двух точек цепи, по которой проходит электрический ток. Для этого примера формула Ома принимает следующий вид:
I = U12/R, где U12 обозначает напряжение между контрольными точками.
С учетом отмеченных на рисунке параметров можно преобразовать итоговое выражение следующим образом:
I = ((ϕ1- ϕ2) ± E)/R12,
где:
- ϕ1- ϕ2 – разница потенциалов;
- Eип – электродвижущая сила, которую характеризуют величина и определенная полярность;
- R12 – полное электрическое сопротивление (проводник + источник ЭДС).
Для пояснения полученного результата следует отметить наличие кулоновских и сторонних сил с векторами ЭДС Eq и Est, соответственно. При перемещении определенного заряда (q) между контрольными точками (1-2) по проводнику будет выполнена работа A12. Зависимости между этими величинами величины можно определить простой формулой:
A12/q = ϕ1 — ϕ2.
Так как ЭДС на участке будет равна работе по перемещению q, справедливо выражение:
Ast/q = E12.
Суммарное значение выполненных действий будет равно напряжению:
U = A12/q + Aип/q = ϕ1 — ϕ2 + E12.
После математического преобразования по закону Ома формула приобретает вид:
I = ((ϕ1- ϕ2) ± E)/R12.
Для корректного применения представленных правил можно рассмотреть пример расчета со следующими исходными данными:
- ЭДС – Eип = 5 V;
- потенциалы в отдельных точках – ϕ1 (ϕ2) = 20V (8V);
- электрическое сопротивление цепи – R12 = 4 Ом;
- сопротивление источника питания – Rип = 2 Ом.
Так как направление тока при замыкании цепи выбирается от большего потенциала к меньшему, по представленной на рис. выше схеме ЭДС берут со знаком «минус». Подставленные в рассмотренную формулу исходные данные помогут сделать следующее вычисление:
I = ((ϕ1- ϕ2) — Eип)/(R12 + Rип) = (20 — 8 — 5)/(4 + 2) = 7/6 ≈ 1,17 А.
Закон Ома в дифференциальной форме
Представленные выше объяснения справедливы для случаев, когда замыкать будут цепь из однородного материала с неизменным поперечным сечением по всей длине. Такими характеристиками обладает обычный провод, сделанный из металла с минимальным количеством посторонних примесей. Качественный резистор обладает аналогичными параметрами. Производители обеспечивают не только равномерное распределение сопротивления в объеме элемента. Дополнительными особенностями конструкции минимизируют реактивные составляющие, чтобы исключить искажения при подключении источника переменного сигнала. Однако даже использование постоянного тока в отдельных ситуациях не позволяет применять для расчетов рассмотренные методики.
Проводник с различным сопротивлением вдоль продольной оси
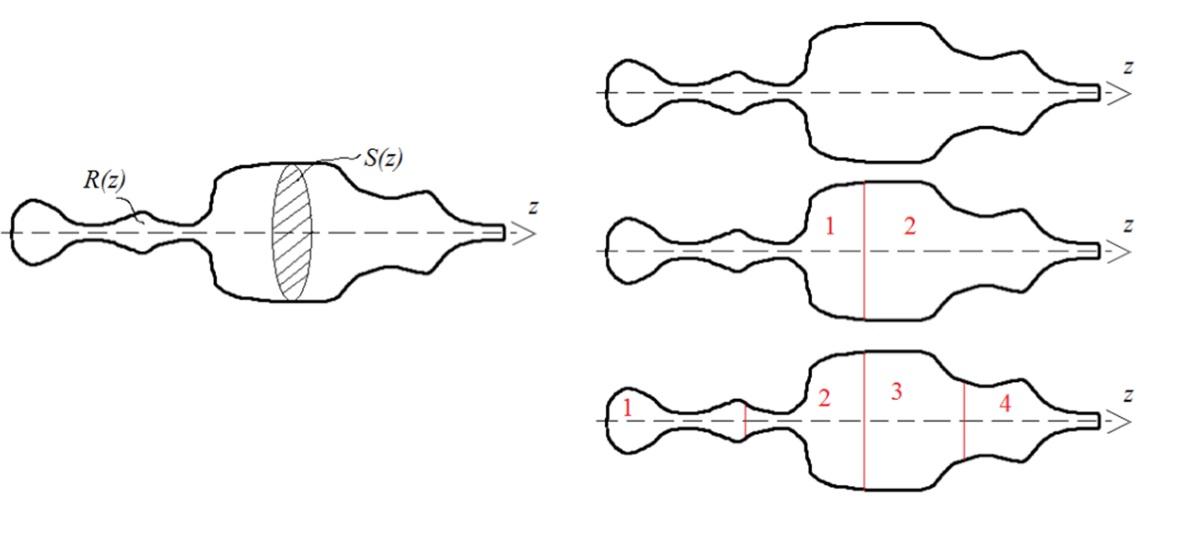
Для удобства можно рассмотреть представленный на картинке образец. В действительности необязательно изменение геометрии проводника по пути прохождения тока. На электрическое сопротивление оказывают влияние различные примеси, существенно различающиеся температурные режимы на протяжении линии определенной цепи.
Для определения электрических параметров классическая формула Ома преобразуется в дифференциальную форму. В данном примере рассматривается изменение площади поперечного сечения S и сопротивления R при перемещении зоны наблюдения вдоль продольной оси. Чтобы упростить расчет, принимают равномерное распределение материала и незначительное содержание посторонних примесей.
Дифференциальный способ, как показано на картинке, заключается в последовательном делении области эксперимента на мелкие участки. Продолжив процесс, на определенном уровне можно получить цилиндр с бесконечно малой толщиной. В таком образце площадь поперечного сечения будет неизменной. Для расчета используют выражение зависимостей:
J = p*E, где:
- J (E) – векторные выражения плотности тока (напряженности);
- p (табличное значение из справочника) – удельная проводимость материала.
Закон Ома в интегральной форме
Для работы с этой методикой можно воспользоваться дифференциальным выражением (J = p*E).
Пояснительные данные к интегральной форме расчета
Базовую формулу преобразуют следующим образом:
- в обе части добавляют множитель, учитывающий элементарный отрезок длины проводника (dL);
- взяв первый интеграл по контрольным точкам, получают итоговое значение для сопротивления: R = p*(L/S);
- совмещают две формулы (1 и 2), выполняют математическое преобразование;
- интеграл второй части определит значение напряжения.
Итоговый результат соответствует определению классического вывода Ома, где взаимная связь u r I обоснована результатом экспериментов (I = U/R).
Интерпретация закона Ома
Чтобы обеспечить перемещение зарядов, нужно замкнуть контур. При отсутствии дополнительной силы ток существовать долго не сможет. Потенциалы быстро станут равными. Чтобы поддерживать рабочий режим цепи, нужен дополнительный источник (генератор, аккумуляторная батарея).
Полный контур будет содержать суммарное электрическое сопротивление всех компонентов. Для точных расчетов учитывают потери в проводниках, резистивных элементах, источнике питания.
Сколько напряжения нужно подать для определенной силы тока, вычисляют по формуле:
U = I * R.
Аналогичным образом с помощью рассмотренных отношений определяют иные параметры схемы.
Когда закон Ома встречается
Создать идеальные условия непросто. Даже в чистых проводниках электрическое сопротивление изменяется в зависимости от температуры. Его снижение минимизирует активность молекул кристаллической решетки, что упрощает перемещение свободных зарядов. На определенном уровне «заморозки» возникает эффект сверхпроводимости. Обратный эффект (ухудшение проводимости) наблюдается при нагреве.
Вместе с тем, электролиты, металлы и отдельные виды керамики сохраняют электрическое сопротивление вне зависимости от плотности тока. Стабильность параметров при поддержании определенного температурного режима позволяет применять формулы закона Ома без дополнительных коррекций.
Полупроводниковые материалы и газы отличаются изменяющимся электрическим сопротивлением. На этот параметр оказывает существенное влияние интенсивность тока в контрольном объеме. Для вычисления рабочих характеристик нужно применять специализированные методики расчета.
Если рассматривается переменный ток, методику расчета корректируют. В этом случае придется учесть наличие реактивных компонентов. При резистивном характере сопротивления можно применить рассмотренные технологии вычислений, основанные на формулах закона Ома.
