Закон Ома для неоднородного участка
Содержание
В простейшем варианте для расчета электрических параметров подразумевают воздействие кулоновских сил, которые обеспечивают перемещение зарядов. Закон Ома для неоднородного участка цепи позволяет учесть дополнительные факторы. Его применение помогает повысить точность вычислений.
Неоднородный участок цепи постоянного тока
Определение основных параметров и процессов:
- перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
- при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
- эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):
q = q0*n*V.
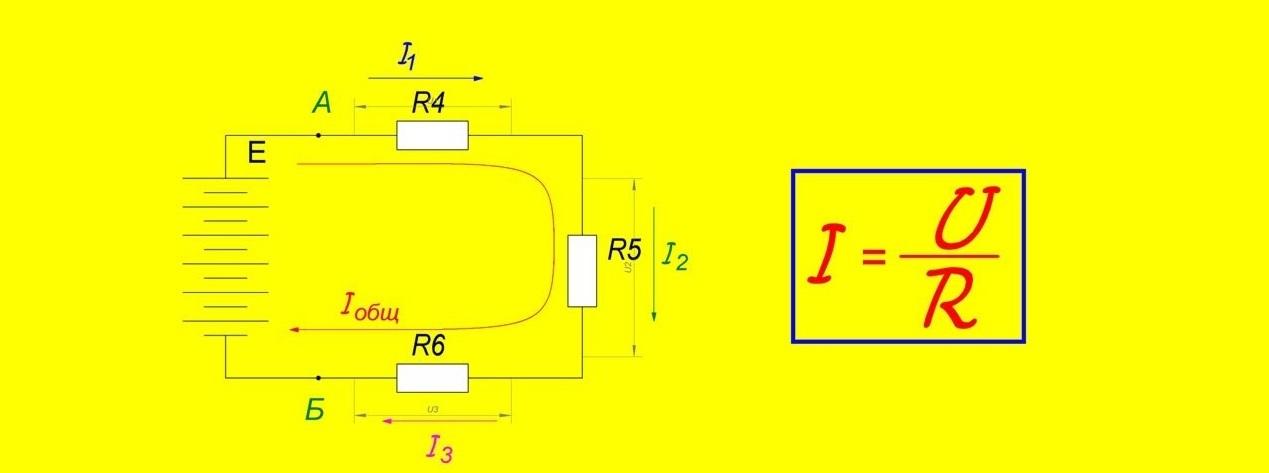
Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.
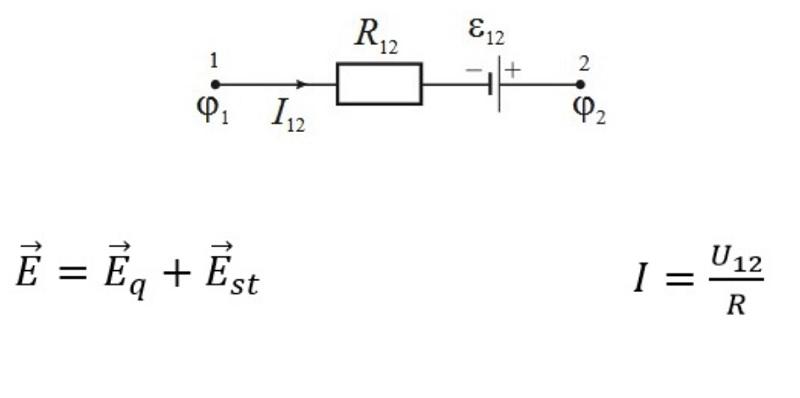
Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).
Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.
Ниже приведены формулы, характеризующие рассмотренный пример:
- A12/q = ϕ1 – ϕ2;
- Ast/q = E12;
- U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
- I = (ϕ1 – ϕ2 + E12)/ R.
Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.
Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:
ϕ1= 20V; ϕ2=10V.
Подставив значения в формулу, можно получить нужный результат:
(20-10+40)/5 = +10А.
Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».
Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:
- кулоновские – Fкул;
- сторонние – Fc;
- сопротивления кристаллической решетки – Fсп.
Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.
Закон Ома для замкнутой цепи
В реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:
I = E/(Rн+Rи).
Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.
Классическая формулировка
Для участка цепи без источника ЭДС достаточно использовать классический закон Ома:
I (сила тока) = U (напряжение) /R (электрическое сопротивление).
Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие. Напряжение определяют по разнице потенциалов на концах проводника:
U = ϕ1 – ϕ2.
Элементарные вычисления показывают взаимные зависимости перечисленных параметров:
- I1 = 24/6 = 4А;
- I2 = 60/6 = 10А.
Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:
I2 > I1.
Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:
- I1 = 24/4 = 6А;
- I2 = 24/12 = 2А.
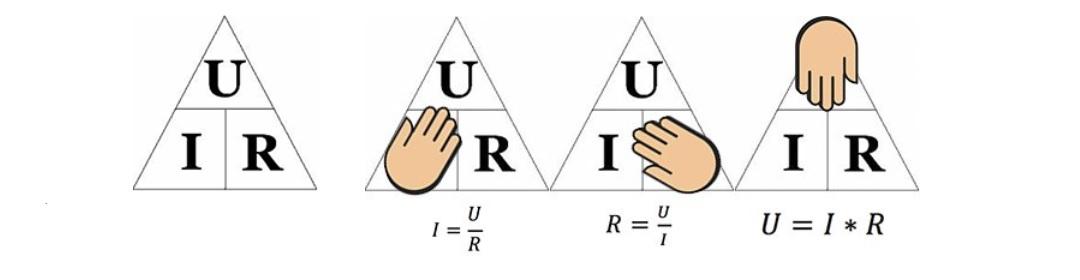
Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.
Эта картинка наглядно демонстрирует взаимное влияние тех основных электрических параметров. С ее помощью можно пояснить особенности практического применения на примере типового проекта домашней сети питания.
В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.
При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.
Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.