Явление резонанса

При определенных условиях возникает явление резонанса, которое сопровождается увеличением амплитуды колебательных процессов. Наглядный пример, известный из детских игр, – раскачивание качелей. Даже при сравнительно небольших усилиях правильно подобранная частота воздействий поднимает тяжелый груз на большую высоту.

Любой механический процесс можно описать с помощью физических определений и специальных формул

Принцип действия

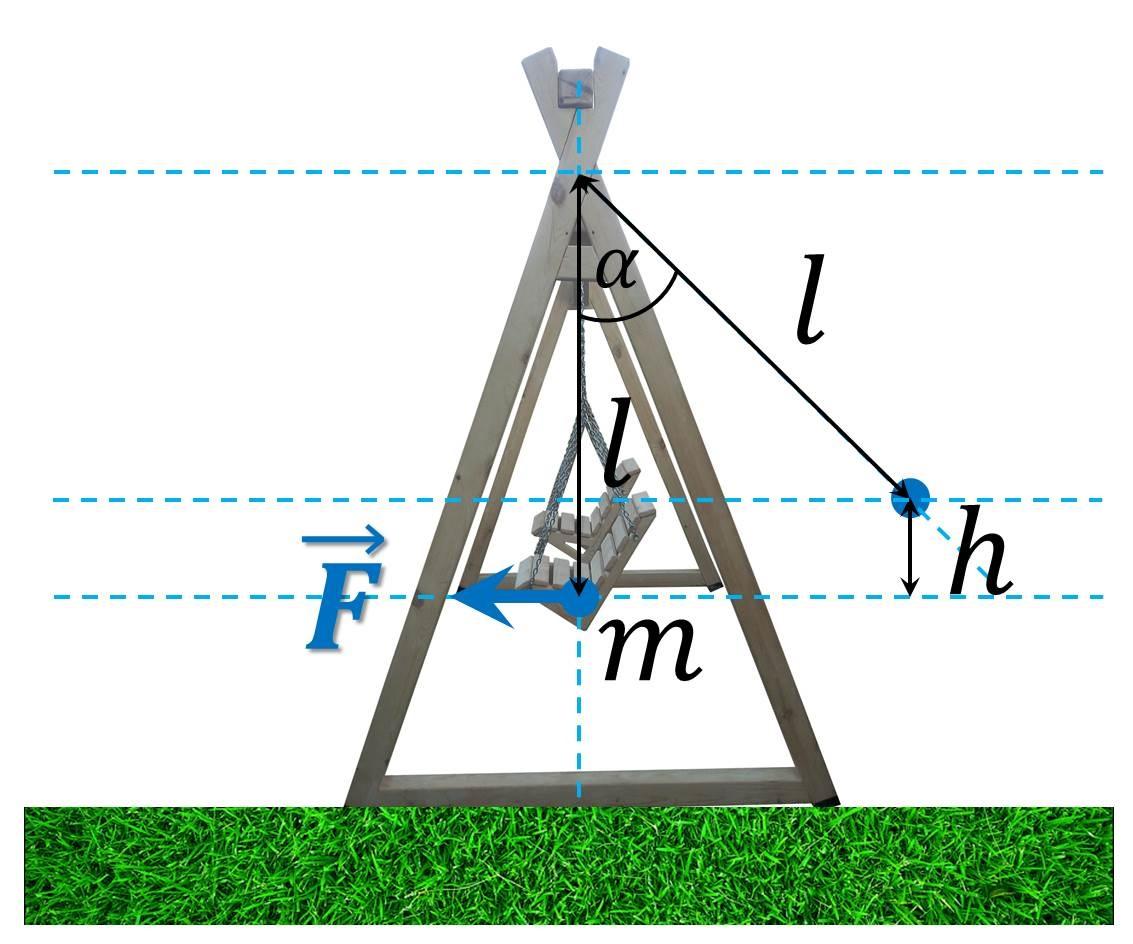
Как показывает простой пример с качелями, система обладает определенной частотой (v). Без вычислений понятно, что удлинение (L) веревки при одном и том же отклонении от вертикали на угол (α) провоцирует увеличение периода колебаний (T).

Резонанс это в физике 11 класса школьной программы определяется как возрастание амплитуды при совпадении собственной частоты конструкции с внешними воздействиями. Хаотичные толчки провоцируют обратный эффект – торможение маятника. Такой результат объясняется противоположным направлением векторов соответствующих сил.

Примеры резонанса в жизни

Рассмотренный выше пример – частный случай. Аналогичные проявления можно обнаружить в разных системах.

Борьба с блоком в дзюдо

Для эффектного броска опытный спортсмен умело повторяет раскачивающиеся движения противника. В определенный момент делает подсечку с толчком в нужном направлении. Грамотное сложение нескольких сил помогает выиграть поединок.

Журналисты утверждают, что Басков расколол бокал силой своего голоса

Для повышения рейтингов устаревающих певцов и анахронических средств массовой информации применяют разные технологии. Однако в самом принципе разрушения хрупкого изделия звуковым колебанием нет ничего удивительного. При широком голосовом диапазоне вполне допустимо совпадение частот. Профессиональный певец в состоянии обеспечить «генерацию» сильных колебаний даже без применения специализированного усилителя.

Разрушение стационарного моста в США (1940 год, штат Вашингтон)

В этом примере крепкую конструкцию уничтожил не многотонный грузовик или испытание атомной бомбы. Совпадение частот потока воздушных масс и моста провоцировало критическую нагрузку и показанные на фото результаты. Данный резонансный случай убедительно демонстрирует необходимость точного расчета для исключения аварийных и катастрофических ситуаций.

Виды резонансных явлений

Рассматриваемые эффекты по-разному проявляются в газовой среде и в твердых телах. Они способны возникать в электрической цепи с реактивными компонентами. При определенных условиях резонансное воздействие разрушит кирпичный дом или разорвет стенки прочного котла паровой машины. Правильное использование этого явления помогает улучшить помехозащищенность радиоаппаратуры, успешно решать другие практические задачи.

Механический резонанс

Для вычисления параметров механической системы можно продолжить изучение маятника. Естественное движение качелей замедляется трением функциональных компонентов, сопротивлением воздуха. Чтобы предотвратить затухание колебаний нужно приложить внешнюю силу (F). Максимальную эффективность обеспечит совпадение частот. Ниже показан алгоритм расчета механического резонанса.

Период (Т) определяется формулой T = 2π√(L/g), где g – константа ускорения свободного падения (≈9,8м/с2). Собственная частота конструкции v = 1/T. Если добавить определение второго закона Ньютона (прямую пропорциональность импульса системы от силы и времени (Δt) воздействия), частоту можно выразить как:

v = ((F* Δt)/m) * N,

где:

• N – количество импульсов;
• m – суммарная масса груза.

Так как энергия в замкнутом контуре сохраняется (идеальный пример без потерь), допустимо использовать следующие пропорции:

(m*v2)/2 = m*g*h = m*g*L*(1-cos α).

Из этих сочетаний простыми преобразованиями получают две формулы для расчетов:

• N = (m/(F* Δt)) * √(2*g*L*(1-cos α));
• t (общее время для выполнения N колебаний) = N*T = (2π*m*L)/(F* Δt)) * √(2*(1-cos α)).

Подставив определенные исходные значения, вычисляют периодичность необходимых резонансных колебаний:

• m=100кг;
• F = 10Н;
• L = 200 см;
• Δt = 1 с;
• N = 34;
• t = 96;
• T = 2,8 с.

Электрический колебательный контур

Явление резонанса может наблюдаться в цепях переменного тока при совпадении частот источника питания (сигнала) и реактивных компонентов контура. В этом случае можно рассматривать электрическое сопротивление, как аналог сил трения в механической системе.

Резонанс токов

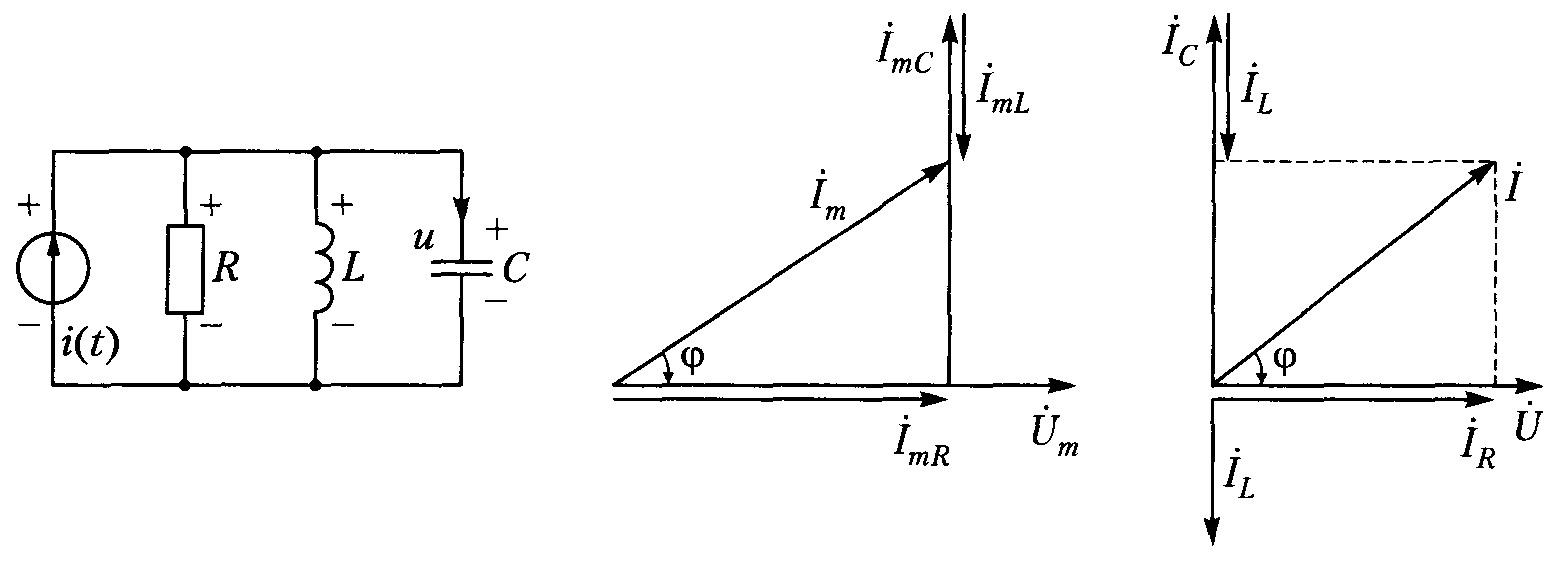
Для создания необходимых условий можно применить параллельное соединение типовых элементов (R, L и C). Если обеспечить равенство импедансов реактивных составляющих, на определенной частоте суммарное значение токов в соответствующих цепях будет больше, по сравнению с током источника питания. Графика на рисунке демонстрирует векторное представление электрических параметров. В этом режиме наблюдается равномерное распределение энергетического баланса колебательного процесса, который поддерживают конденсатор и катушка индуктивности.

Для вычислений нужно уточнить влияние каждого компонента. Емкость создает препятствие прохождению тока, определяемое формулой:

Xc = 1/(2π*f*C),

где:

• Xc – сопротивление;
• f – частота;
• С – емкость.

Индуктивная составляющая определяется следующим образом:

XL = 2π*f*L.

Полное сопротивление контура:

Z = √R2 + (2π*f*L — 1/(2π*f*C)2.

При равенстве реактивных компонентов несложно сделать вывод о том, что 2π*f*L = 1/2π*f*C. Частоту, на которой появится резонанс, вычисляют по формуле:

Fрезонанса = 1/2π * √ (L*C).

Условия резонанса напряжений в последовательном контуре

Сложные колебательные структуры

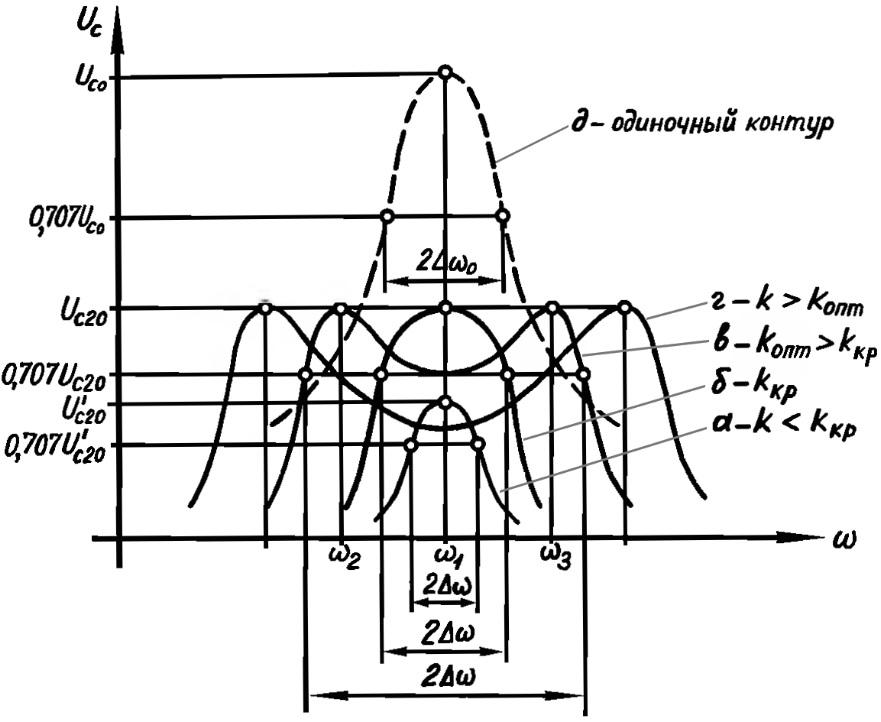
Если применить трансформатор для образования связи между двумя колебательными контурами, расчет усложняется. Для создания необходимых условий обеспечивают равенство реактивных составляющих.

Резонансные кривые связанных контуров

Рисунок демонстрирует изменение полосы пропускания при разных значениях коэффициента (К), определяющего передачу напряжения. При увеличении этого параметра выше критического уровня (K>Ккр) образуется двугорбая кривая. Максимальная ширина полосы пропускания обеспечивается при К = 0,7*Кмакс. Дальнейшее усиление связи формирует провал в средней части.

Нелинейные системы

Если отсутствуют симметричные реакции на сторонние воздействия, резонансные явления проявляются особым образом. В частности, наличие в цепи катушки с ферритовым сердечником существенно усложняет точный расчет. В подобных материалах магнитные свойства определяются нелинейным распределением элементарных компонентов.

Польза и вред резонанса

Изложенные сведения применяют для решения разных прикладных задач. Выяснив, что такое резонанс в физике, можно с помощью малых внешних сил развивать большую полезную мощность. Точный расчет предотвратит вредные воздействия, ухудшающие функциональное состояние механических аппаратов и электротехнических схем.

Положительный эффект

Изложенные принципы объясняют применение резонанса для обработки сигналов. Точный расчет компонентов и коэффициента связи контуров поможет создать эффективный фильтр, пропускающий электромагнитные колебания в определенном частотном диапазоне.

Последовательный контур можно использовать для повышения напряжения, если сеть питания неспособна поддерживать необходимый уровень. Правильно подобранный конденсатор обеспечит плавное включение привода, что продлит срок службы оборудования и снизит нагрузку на электростанцию.

С помощью перфоратора сверление отверстий в прочных железобетонных стенах выполняется быстро и без чрезмерных усилий

Отрицательное воздействие

Резонанс разрушает прочные конструкции, функциональные узлы, механизмы. При ошибках в расчетах это явление ухудшает работоспособность электрических схем. Особо сильные воздействия провоцируют аварийные ситуации.

В качестве примера можно привести резонансные частоты, которые учитывают при создании санитарных, технических и производственных нормативов:

• стоящий, сидящий и лежащий человек: 4-13 (16-26), 4-7 и 2,5-3 Гц, соответственно;
• голова: 18-35 Гц;
• грудная клетка: 2,5-4 Гц;
• брюшная полость: 6-9 Гц.

При совпадении частоты вибраций (от инструмента, работающего оборудования) ухудшается состояние нервной системы, провоцируются паталогические изменения в организме.

Борьба с резонансом

Для уменьшения и блокирования вредных воздействий применяют специальные меры. Чтобы предотвратить разрушение моста, командир приказывает подразделению шагать «не в ногу» на соответствующем участке маршрута. Увеличение частоты вращения рабочих инструментов предотвращает профессиональные заболевания. Успешно решать другие задачи можно с помощью рассмотренной методики расчетов.

Видео

Автор:

Гaличeв Илья Виктoрoвич