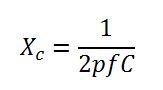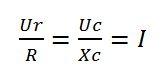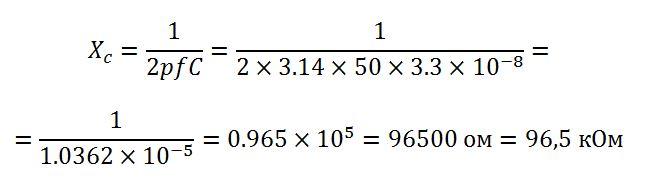Емкостное сопротивление
Содержание
Использование ёмкости в цепи постоянного тока знакомо каждому электронщику. В этом случае работа детали описывается сравнительно простыми физическими законами. Несколько сложнее дела обстоят с переменным током, ведь при таком применении ёмкости уже возникает необходимость учитывать реактивное сопротивление.
Активная и реактивная составляющие
Формула ёмкостного сопротивления
При подаче на обкладки конденсатора переменного напряжения ток через этот элемент первоначально стремится к максимальному значению. По мере заряда прибора он постепенно снижается. В то же время вольтаж ведёт себя иначе, т.е. плавно возрастает от нуля до максимального значения.
Подобный эффект вызван ёмкостным сопротивлением. Оно зависит как от строения самого электронного прибора, так и от характеристик поданного на него переменного напряжения.
Формула расчёта сопротивления
Где:
- XC – реактивное сопротивление, ом;
- p – 3,14;
- f – частота переменного напряжения, приложенного к обкладкам, Гц;
- C – ёмкость, Ф.
Векторное представление ёмкости
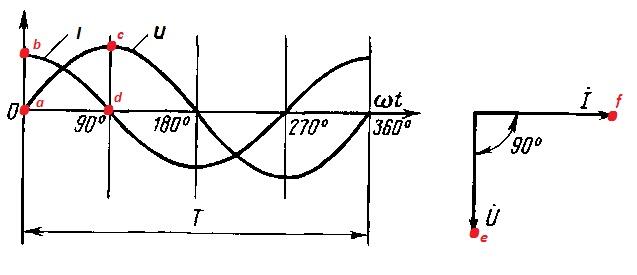
Для простоты понимания процессов, происходящих в конденсаторе под действием источника переменного тока, удобно воспользоваться векторным представлением ёмкости.
Векторная диаграмма
В начальный момент зарядки конденсатора потенциал U на его обкладках равен нулю (точка a). В то же время ток I имеет своё максимальное значение (точка b). На этом этапе уже заметно отставание. Ток начинает снижаться со своей пиковой величины (участок bd). Напряжение в этот момент ещё не выросло и только подбирается к своему максимуму (ac).
Подобное отражается и на диаграмме справа. В момент, когда вольтаж U имеет своё наименьшее значение (e), ток I только начинает переходить в отрицательную область (f).
Емкостное сопротивление
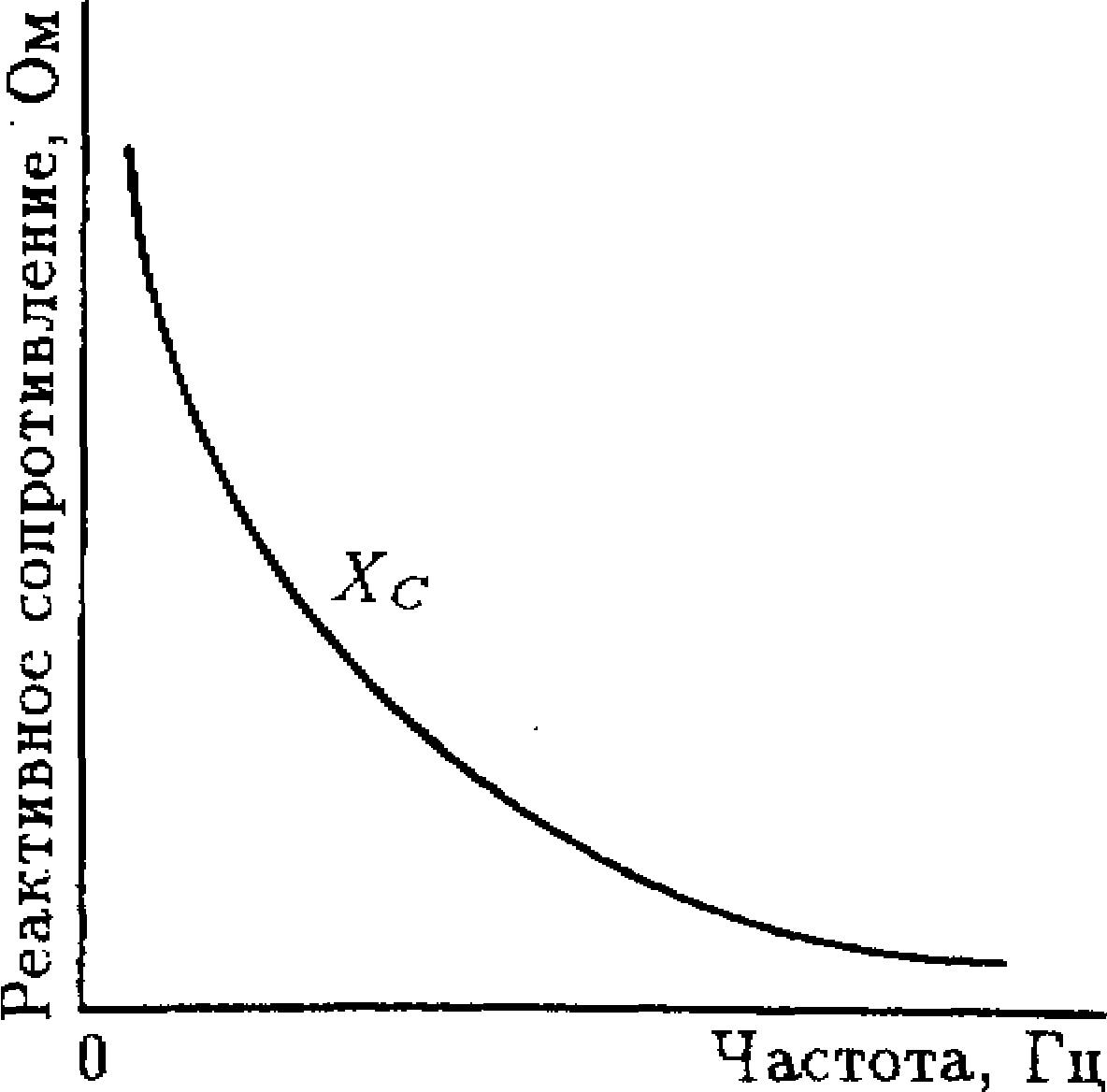
Ёмкостное, оно же реактивное, сопротивление принципиально зависит от частоты напряжения. Данная связь хорошо видна на графике, приведённом ниже. Чем выше частота, тем меньше реактивное сопротивление. Очевидно это и из вышеприведённой формулы. Переменная f (частота) стоит в знаменателе. Поэтому с её увеличением Xc будет уменьшаться.
Зависимость от частоты
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
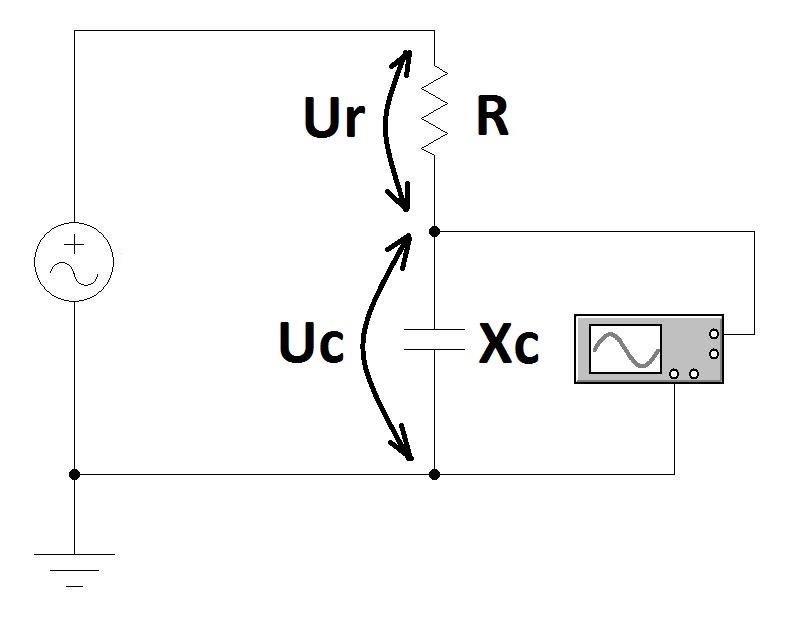
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
Косвенное измерение
Единицы измерения
Для правильного проведения всех расчетов важно понимать, какие величины в них используются, и что они обозначают:
- Ёмкость – ед. изм. фарад, Ф;
- Напряжение – вольт, В;
- Сопротивление, в т.ч. и реактивное – ом, Ом;
- Частота – герц, Гц;
- Ток – ампер, А.
Пример расчета емкостного сопротивления
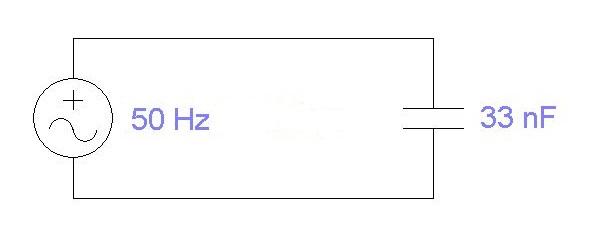
Для расчета понадобится большинство из перечисленных физических величин. Они обозначены на схеме и в качестве примера имеют следующие значения:
- частота f = 50 Гц (типичная бытовая сеть);
- ёмкость C = 33 нФ = 0,000000033 Ф = 3,3*10-8 Ф;
Схема для примера
Реактив будет рассчитываться по вышеописанной формуле:
Xc = 1/(2pfC).
В таком случае сопротивление конденсатора в цепи переменного тока равно 96,5 кОм. Если расписать все вычисления, то получится следующее.
Пример расчёта
Сама по себе формула не вызывает сложности. Однако для проведения вычислений необходимы знания школьного курса алгебры, т.е. умение работать со степенями, дробями и прочими алгоритмами математики. На практике имеет смысл немного схитрить. Чтобы каждый раз не городить сложные вычисления, можно воспользоваться одним из онлайн калькуляторов из сети Интернет. Подобные ресурсы позволяют произвести комплексный расчёт и выяснить некоторые другие параметры цепи.
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C.
RC цепь
Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU. Здесь U – напряжение источника питания.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
