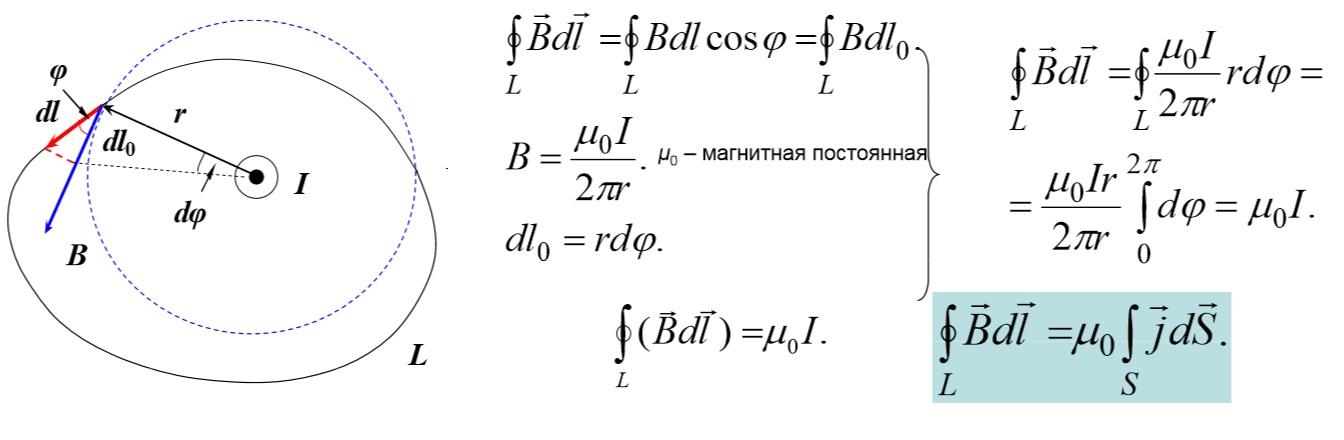Закон полного тока
Содержание
В радиотехнических схемах применяют трансформаторы и другие изделия, функциональность которых определена индуктивными характеристиками. В данной публикации представлен закон полного тока, который используют для предварительных расчетов и коррекций устройств с магнитными компонентами.
Определение полного тока
Сутью данного закона является определение взаимной связи между электрическим током и образованным его протеканием магнитным полем. Эта особенность выявлена экспериментальным путем в первой половине XIX века. Позднее была создана формулировка, устанавливающая закон полного тока для магнитного поля. Классическое определение приведено ниже. Однако начинать изучение темы следует с базовых принципов.
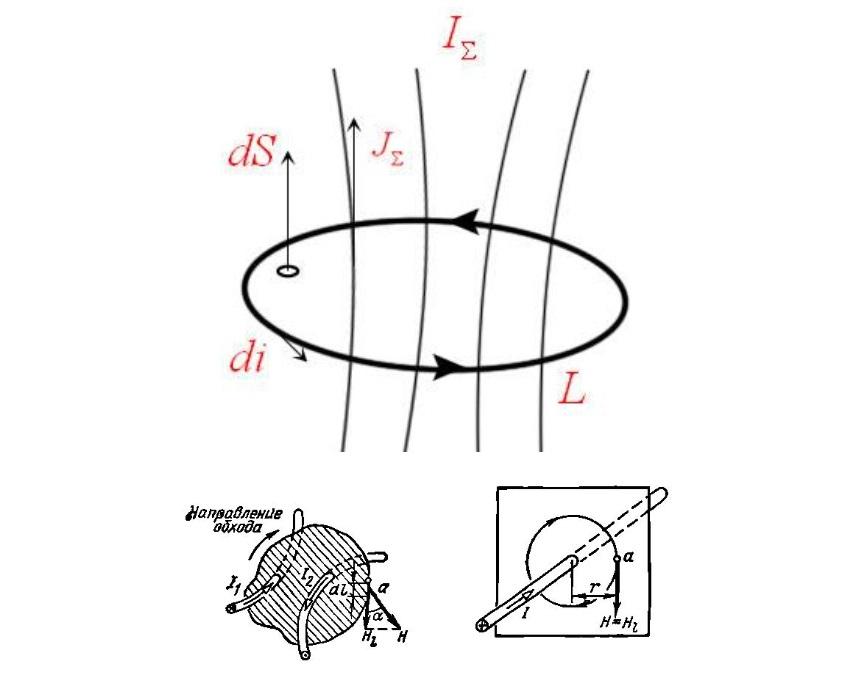
На рисунке отмечены следующие компоненты:
- I∑ – суммарный (полный) ток;
- S – пронизываемая (dS – элементарная) площадка;
- dL – элементарный линейный участок.
- J∑ – плотность распределения токов;
- L – кольцевой замкнутый контур;
- H – напряженность магнитного поля в векторном представлении.
Магнитное напряжение вдоль контура
В представленном примере для изучения берут проводники, через которые пропускают электрический ток. В совокупности они образуют сечение с мнимой площадью (S), которая ограничена неким контуром. Пользуясь классическим правилом «буравчика», несложно установить направление вектора (di или Н). Понятно, что в данном случае рассматривается дискретная величина. Вектор магнитной напряженности и полный ток связаны следующей формулой:
I∑ = ∫L*H*dL.
Полный ток
Из приведенного соотношения видно, что сумма токов равна перемещению вектора напряженности магнитного поля по замкнутому контуру. Его циркуляция описывается интегралом приведенных выше компонентов. Из рассмотренных пропорций несложно сделать вывод о том, что полный ток будет зависеть от плотности, контура и элементарной площадки:
I∑ = ∫S*J*ds.
Магнитодвижущая сила
Представленный закон применяют для расчета рабочих характеристик разных устройств:
- одно,- и трехфазных трансформаторов с подключением к сети 220 (380) V, соответственно;
- электродвигателей постоянного тока;
- катушек с тороидальными сердечниками;
- электрических приводов реле и клапанов;
- аналоговых измерительных приборов и датчиков;
- электромагнитов, которые установлены в подъемных механизмах, системах водоочистки.
Для подробного изучения подойдет несложный пример. В цепи обеспечивается перемещение тока по замкнутому контуру с применением катушки индукции. Созданная магнитодвижущая сила (F) будет зависеть от силы тока (I) в проводнике и количества сделанных витков (W):
F = I * W.
По классическим определениям, ток в цепи появляется при создании разницы потенциалов между точками подключения источника ЭДС. Подобным образом показанная выше сила F провоцирует образование магнитного потока. В данном случае аналогичным образом можно использовать не только правило буравчика, но и технологии расчета цепей. Необходимо только корректно применять отдельные понятия. Так, электрическому сопротивлению соответствует магнитный аналог.
При разделении такого контура на два сегмента справедливым будет следующее выражение:
Н1*L1 + H2*L2 = I *W,
где Н1 и H2 (L1 и L2) напряженность (длина) соответствующих частей.
Последовательным преобразованием можно получить удобную для практического применения формулу закона полного тока:
- H1 = B1/ma1;
- B1 = Ф/S1;
- H2 = B2/ma2;
- B2 = Ф/S2;
- I*W = Ф*L1/ma1*S1 + Ф*L1/ma1*S1 = Ф*Rm1 + Ф*Rm2.
Кроме площади поперечного сечения (S), здесь приведены магнитные параметры разных участков (1 и 2):
- Ф – поток;
- В – индукция;
- ma – проницаемость.
Из этого выражения нетрудно получить значение магнитного сопротивления для каждого участка:
Rm = L/ma*S.
По аналогии с формулой Ома для электрических цепей можно вычислить магнитное напряжение:
U = Ф * Rm.
C учетом частоты питающего сигнала (w) магнитный поток будет зависеть от силы тока и суммарного сопротивления участков цепи:
Ф = (I*w)/(Rm1+Rm2) = (I*w)/∑Rm.
Определение закона полного тока
Важные выводы и пояснения:
- напряженность зависит от источника тока;
- индукция выполняет силовые функции воздействия на движущиеся по цепи заряды;
- параметры поля формируются магнитными свойствами определенной среды.
На практике усиление тока сопровождается пропорциональным изменением поля (магнитной индукции). Базовое правило справедливо при рассмотрении цепей, созданных из серебра, влажного или сухого воздуха, других материалов.
Измененные правила действуют в железе или иной среде с выраженными ферромагнитными свойствами. Именно такие решения применяют при создании трансформаторов и других изделий для улучшения потребительских характеристик.
Для упрощения следует начать изучение физических величин и расчетов на примере нейтральной среды. При отсутствии ферромагнитных параметров можно изобразить магнитное поле несколькими замкнутыми линиями длиной L. В этом случае полный ток (I) будет зависеть от индукции (B) следующим образом:
I = (B*L)/м.
Здесь m – магнитная постоянная, которая в стандартной системе единиц измерения приблизительно равна 1,257*10-7 Генри на метр (Гн/м).
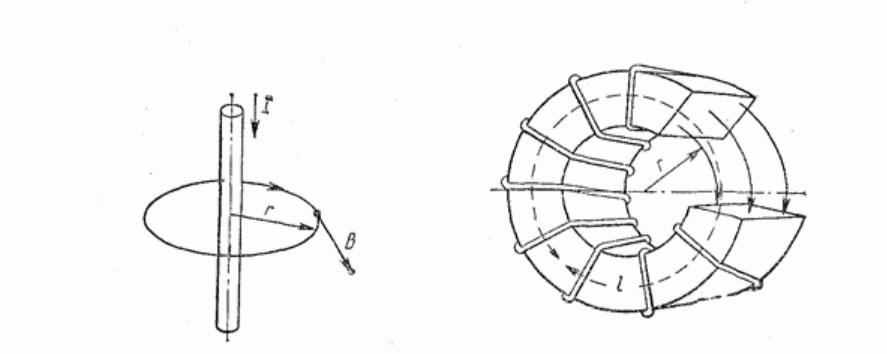
Поле формируется перпендикулярно прямому длинному проводнику. Его линии образуют набор из множества окружностей. Центр каждой из них соответствует продольной оси проводника. Расстояние от нее до кольца – r. Длину (L) вычисляют по стандартной геометрической пропорции:
L = 2π*r.
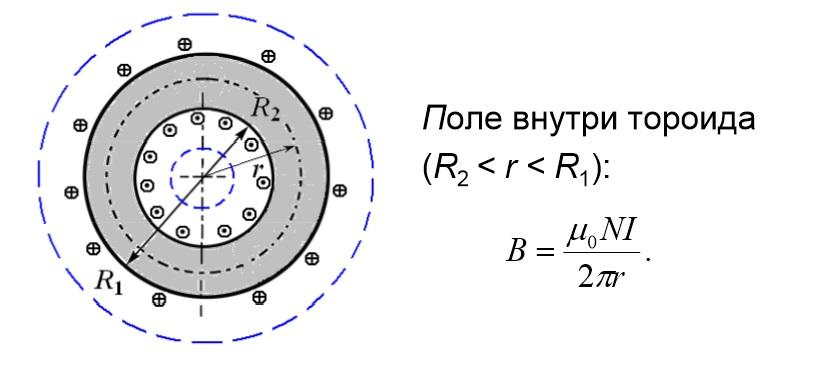
Если разместить витки симметрично на тороидальном сердечнике из электрически нейтрального фарфора для устранения искажений, линии магнитного поля будут проходить внутри равномерно. Кольца, как показано на рисунке с вырезанным сегментом, образуют замкнутые контуры. В такой конструкции обеспечивается неизменность индукции. Для каждой отдельной линии можно пользоваться формулой:
B*L = B* 2π*r = m*I.
Суммарное значение (полный ток) получают умножением на количество витков (N).
На основе приведенных данных нетрудно вычислить индукцию, которая будет создана внутри нейтрального тороидального кольца при определенной силе тока:
B = m*(I*N/L).
Эта пропорция позволяет сделать определение удельного полного тока:
(IN)o=(I*N)/L.
Зная размеры тора и другие исходные параметры, вычисляют индукцию у внутреннего и наружного края. При необходимости делают коррекции с помощью изменения толщины кольца, количества витков.
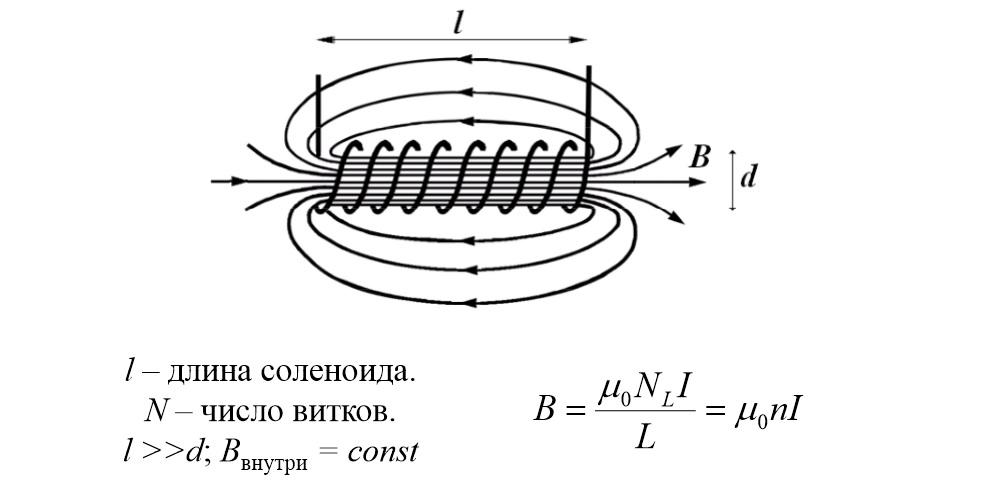
Если на основу из ферромагнитного материала намотать две обмотки (изолированные), будут создан наглядный образец для измерений. Изменяя силу тока в одном проводнике, можно наблюдать за изменением электродвижущей силы по подключенному к другой паре выводов прибору.
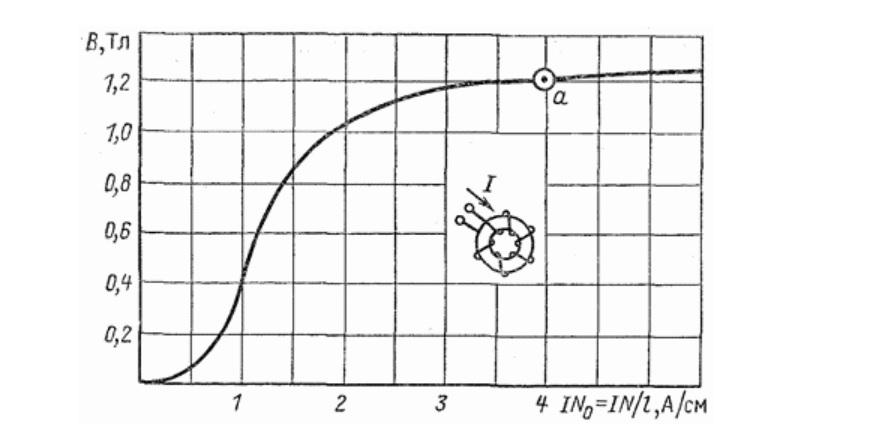
На графике приведены результаты эксперимента при использовании кольца, сделанного из железа с минимальным количеством примесей. Если применить закон полного тока для рассмотренного выше примера с нейтральным сердечником в точке «а», должно получиться приблизительно 5*10-4 Тл. Между тем в действительности напряженность составляет для этой силы тока 1,2 Тл при одинаковых размерах тока и количестве сделанных витков.
Корректируют вычисления с учетом поправочного коэффициента – магнитной проницаемости. Следует подчеркнуть, что это параметр не линейный. Максимальный полезный эффект наблюдается при относительно небольших значениях силы тока. Значительный спад после порогового уровня насыщения ограничивает практическое применение рассмотренных свойств.
Формула закона полного тока
В этом разделе приведены формулы для уточненных расчетов и примеры типовых конструкций. Для интегральных вычислений вполне подходит закон Гаусса, который применяют в электростатике.
Пояснения:
- L – обозначает замкнутый контур, созданный по произвольной траектории;
- векторы В и r направлены перпендикулярно;
- dl (dl0) – элементы произвольной части (силовой линии), соответственно;
- ϕ – угол между элементами.
Из формулы на рисунке понятно, что циркуляция вектора индукции не равняется нулю. Такие поля называют «соленоидальными» или вихревыми. В отличие от электродинамики, в данном случае отсутствуют потенциальные характеристики. Как и в базовом определении, полный ток определяется циркуляцией магнитной индукции (векторное выражение) по контуру произвольной формы, окружающему сумму токов.
В этом примере n – число витков обмотки на единицу длины основы.
Параметры:
- количество сделанных витков – N;
- внешний, внутренний и произвольный радиусы – R1, R2 и r.
Рассмотренные методики расчетов применяют с учетом реальных условий. Особое значение при выборе компонентов конструкций уделяют ферромагнитным свойствам сердечника. Проводники для обмоток выбирают с запасом, учитывая максимальную силу тока источника.