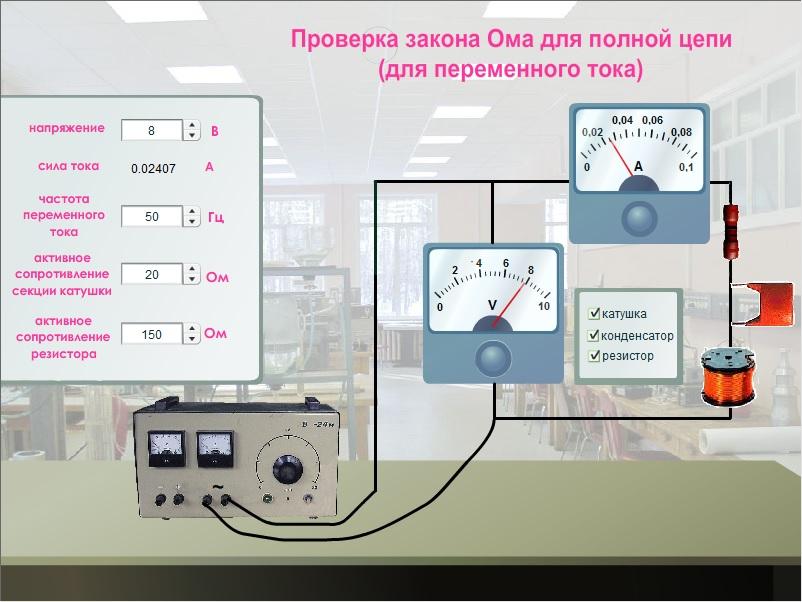
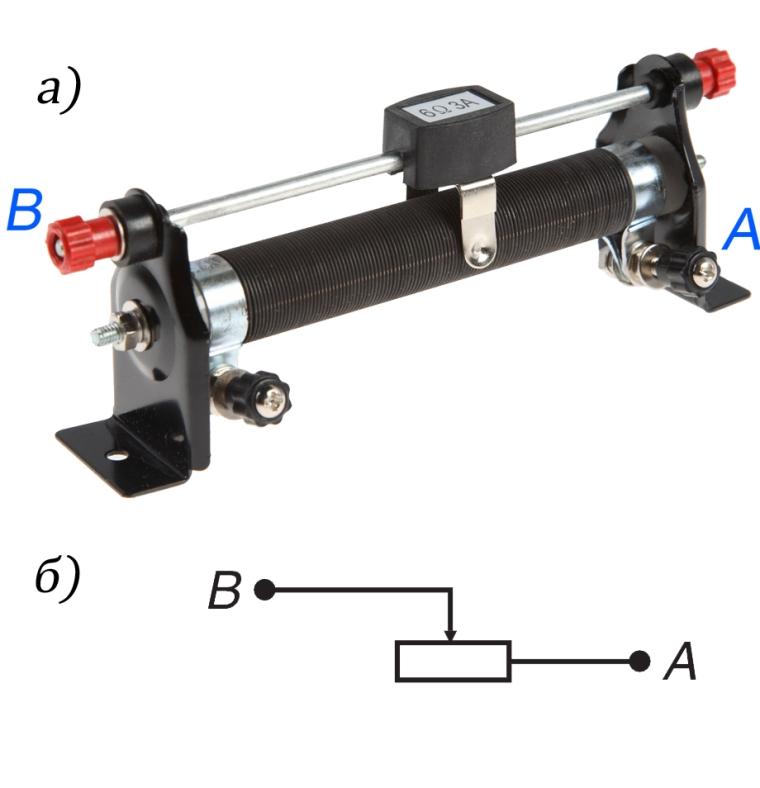
Закон Ома для переменного тока
Содержание
Чтобы правильно подключить нагрузку, создать защитную схему и решить другие задачи в электротехнике применяют закон Ома для переменного тока. Созданные на основе базовых правил формулы удобны для быстрого вычисления основных параметров: силы тока, напряжения, сопротивления. В данной публикации рассматриваются переменные сигналаы, поэтому особыми дополнениями учтены частотные зависимости.
Корректность теоретических знаний можно подтвердить опытным путем
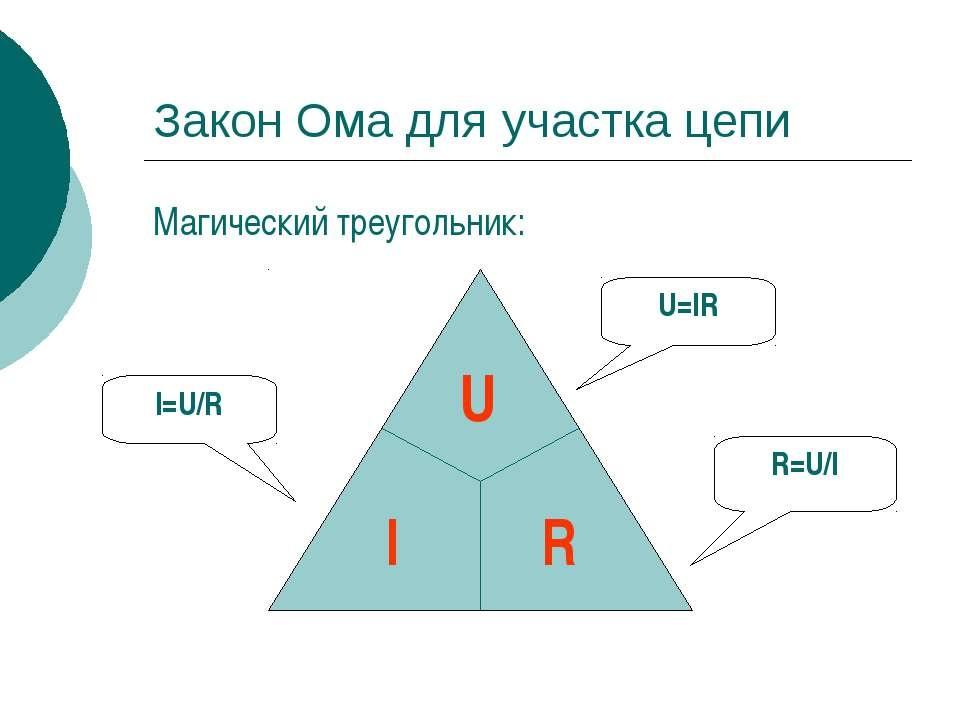
Закон Ома для участка цепи
По классической формулировке зависимость электрических параметров описывают следующим образом: ток на участке цепи (I) прямо пропорционален разнице потенциалов между контрольными точками (напряжению, U) и обратно – сопротивлению (R). Записать приведенное определение можно с применением типовых обозначений:
I = U/ R.
«Магический» треугольник поможет запомнить основные формулы
Эти выражения действительны для любого токопроводящего участка схемы. Пример с резистором, через который пропускается постоянный ток, можно использовать для демонстрации элементарного алгоритма вычислений:
- исходные данные: R = 25 Ом, U = 8 B;
- для расчета тока используют приведенную формулу: I = U/ R = 8/ 25 = 0,32 А;
- если известен ток (I = 1,5 А) и сопротивление (R = 15 Ом), без вольтметра можно узнать напряжение на выводах резистора: U = I *R = 1,5 * 15 = 22,5 В.
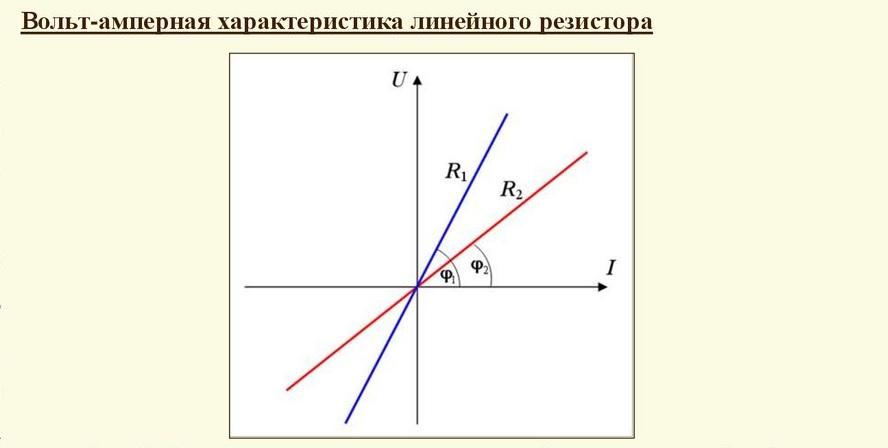
Рассмотренные сведения применяют для коррекции электрических параметров. Так, если нужно увеличить напряжение, выбирают сопротивление с большим номиналом. Одновременно обеспечивают стабилизацию тока. Если построить диаграмму с измеренными значениями тока и напряжения по вертикальной и горизонтальной оси, график получится в виде прямой линии. Эта форма подтверждает отсутствие активных составляющих процесса.
Вольтамперная характеристика
В приведенном на рисунке примере R1>R2. Для прохождения сильного тока приходится увеличивать напряжение либо уменьшать сопротивление контрольного участка.
Закон Ома для полной цепи
В реальных условиях нужно учитывать сопротивление источника тока (Rи). В этой ситуации действуют рассмотренные выше принципы. Однако базовую формулу нужно изменить следующим образом:
I = E/ (R + Rи), где E – это электродвижущая сила (ЭДС) аккумулятора. После преобразования можно получить выражение:
Rи = (E/I) – R.
Закон Ома для цепи переменного тока
При подключении нагрузки к такому источнику следует учитывать наличие в цепи компонентов с реактивными составляющими электрического сопротивления, конденсаторов и катушек индукции. Закон Ома для цепей переменного тока действует исключительно для амплитудных и эффективных значений напряжения и тока.
Распределение фаз в цепи с активным сопротивлением
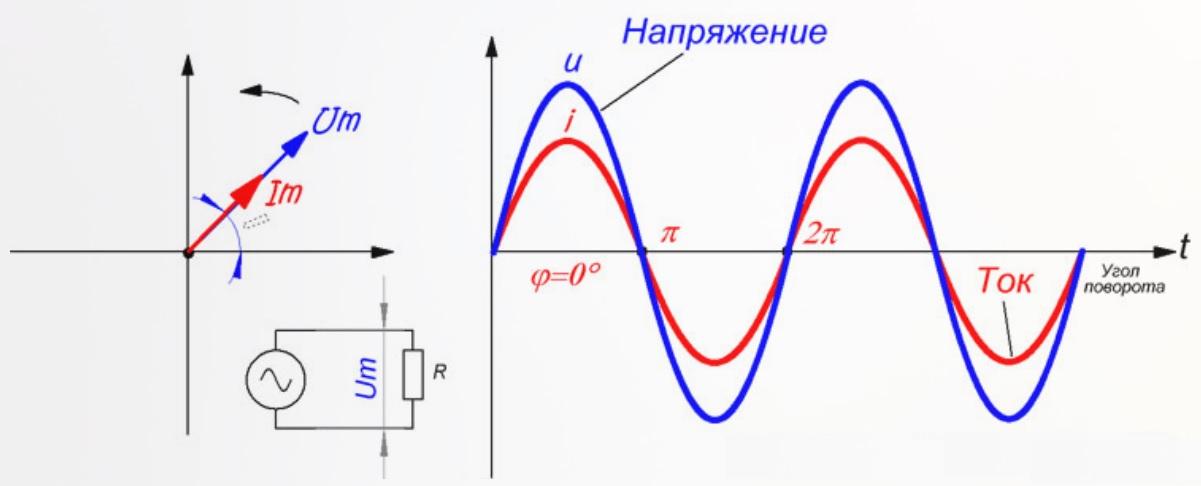
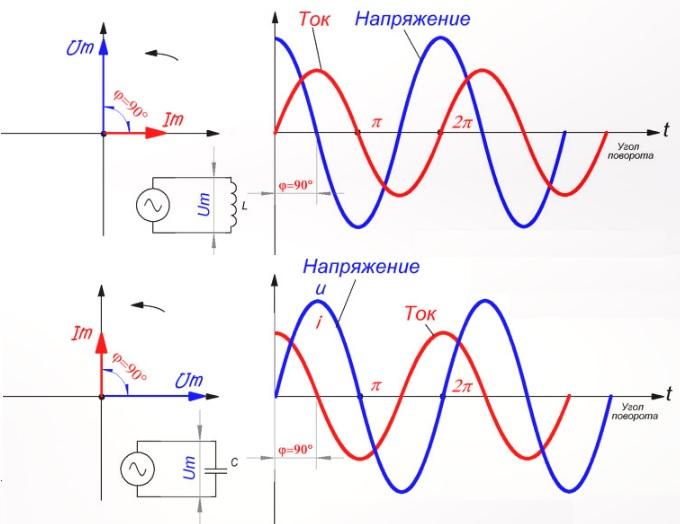
В представленной на рисунке схеме реактивные составляющие отсутствуют. Для этого случая векторы тока и напряжения совпадают по фазе. Расчеты с активным сопротивлением можно выполнять с применением рассмотренных выше формул.
Индуктивная и емкостная нагрузки
При подключении элементов с реактивными характеристиками угол между векторами составляет 90°. В схеме с индуктивностью (емкостью) ток будет отставать от напряжения по фазе либо опережать соответственно. Для расчета напряжения можно применять следующие формулы (w – циклическая частота):
- UL = I * w*L;
- UC = I/ (w*C);
- ХL = w*L;
- XC = 1/(w*C).
Для полной цепи надо учесть суммарное значение сопротивления – Z. В следующем перечне приведены методы вычислений при наличии в цепи типовых комбинаций пассивных компонентов:
- резистор и катушка индуктивности (последовательное соединение): I = U/ √(R2 + (w*L)2);
- конденсатор с емкостью С и резистор: I = U/√(R2 + (1/w*C)2);
- цепочка RLC: I = U/√(R2 + (w*L + 1/w*L)2).
Сдвиг фаз можно представить следующими выражениями:
- tg ϕ = (UL — UC)/ UR = (ХL — XC)/R;
- cos ϕ = UR/U = R/ Z.
Для расчета активной мощности (Pа) в нагрузке применяют действующие значения тока (Iд) и напряжения (Uд):
Pа = Iд * Uд * cos ϕ.
Последний множитель фактически определяет количество потребляемой электроэнергии. Остаток расходуется на обменные процессы, нагрев соединительных проводов.
Отдельно следует рассмотреть резонанс. Это явление сопровождается резким увеличением силы тока в цепи при совпадении частоты сигнала (wc) с частотой созданного колебательного контура (wк). В подобной ситуации не исключено повреждение компонентов схемы и проводников.
Обозначенные условия создает увеличение сопротивления в цепи, которое обеспечивается равенством реактивных составляющих:
ХL = w*L = XC = 1/(w*C).
Частоты совпадают в следующем случае (последовательное соединение):
wc = wк = 1/√(L*С).
Напряжения на конденсаторе и катушке становятся равными по амплитуде, но противоположными по фазе. Ток определяется с учетом базовых определений закона Ома:
I = U/Z = U/ √ R2 + (2π * w * L — 1/2π * w * C)2.
Трактовка и пределы применимости закона Ома
Для корректных расчетов следует учесть ограниченность действия рассмотренных методик. Законом Ома установлены базовые зависимости, которые сохраняются в сравнительно узком частотном диапазоне. Подразумевается применение компонентов с «идеальными» параметрами. Паразитные характеристики, взаимное влияние и отдельные внешние воздействия не учитываются.
Сверхпроводимость
В следующем списке приведены примеры, когда формулы закона Ома не описывают физические процессы с достаточной точностью:
- При значительном понижении температуры уменьшается амплитуда колебаний компонентов молекулярной решетки металлов. Это улучшает условия для прохождения заряженных частиц. На определенном уровне возникает сверхпроводимость, которая характеризуется минимальными потерями энергии в проводнике.
- В диапазоне сверхвысоких частот следует учитывать инерционные характеристики заряженных частиц. Определенное значение приобретают поверхностные токи.
- По мере нагрева на определенном уровне проводимость материала изменяется нелинейно, что исключает возможность применения представленных формул.
- Высоковольтное напряжение провоцирует пробой диэлектрика.
Нелинейные элементы и цепи
Как отмечено в предыдущем разделе, калькулятор и элементарные технологии расчета в отдельных ситуациях непригодны.
График изменения сопротивления
На рисунке приведены результаты эксперимента с типовой лампой накаливания. Видно, что при увеличении напряжения сопротивление изменяется нелинейно. Данное явление сопряжено с нагревом вольфрамовой нити. Для подобных ситуаций необходимы сведения о значениях проводимости в отдельных точках графика. Например, можно использовать тангенс угла α по отношению к горизонтальной оси. В этом случае статическое электрическое сопротивление для определенного места (Rст) рассчитывают по формуле:
Rст = Uα/Iα = tg α.
Также применяют значение, эквивалентное минимальному изменению тока и напряжения (ΔI и ΔU соответственно). По этой методике Rст = ΔU / ΔI = tg ϕ, где ϕ – угол между касательной в контрольной точке и осью абсцисс.
Нелинейные элементы
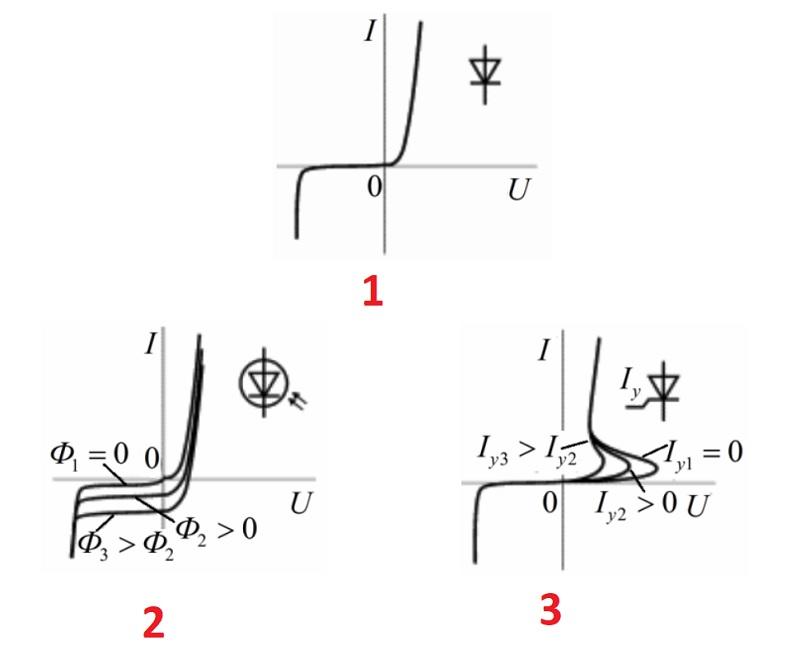
На первом рисунке показана вольтамперная характеристика серийного диода. График подтверждает смещение полупроводникового перехода в зависимости от приложенного напряжения. Хорошо видно, как на горизонтальном участке существенное изменение потенциала сопровождается незначительной реакцией силы тока.
Второй рисунок демонстрирует зависимость характеристик от уровня светового потока (Ф). Стандартный фотодиод функционирует в области обратного смещения p-n перехода. Это наглядный пример двухполюсного радиотехнического компонента с нелинейными параметрами.
На последнем рисунке изображена вольтамперная характеристика тиристора. Работой этого устройства управляют с помощью дополнительной области, созданной в полупроводниковом переходе. Аналогичные по сути решения применяют в транзисторах.
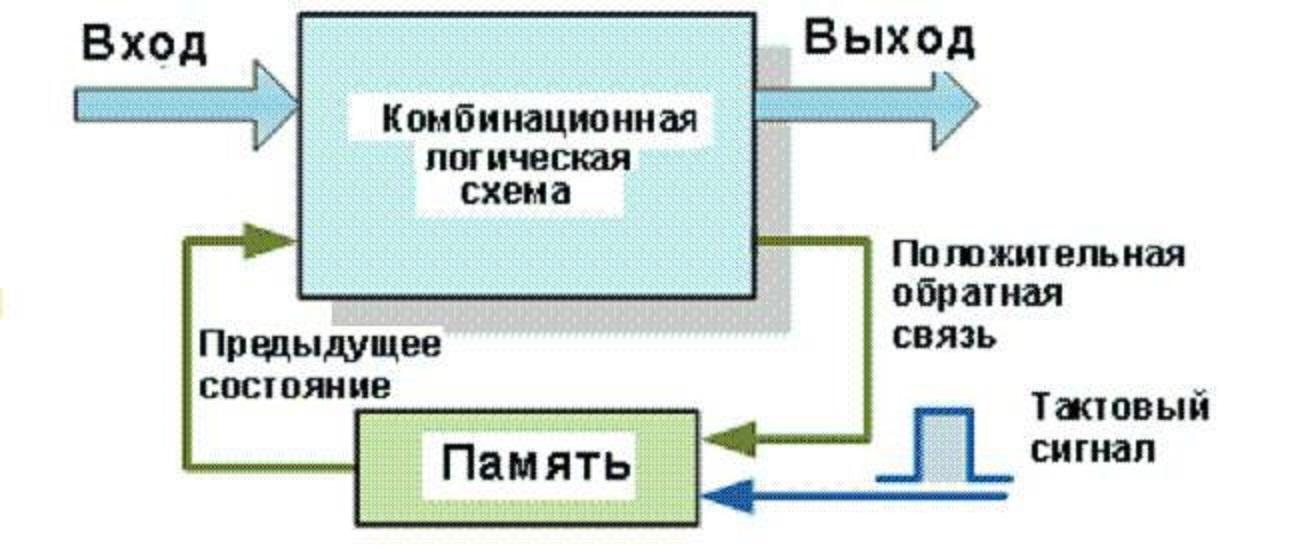
Цепи, которые будут содержать подобные компоненты, называют нелинейными. При расчетах учитывают особенности ВАХ, время переключения. Определенное значение имеет класс изделия. К безынерционным относят элементы с быстрой реакцией на управляющие воздействия.
