Резонанс в электрической цепи

При определенном сочетании частоты сигнала и реактивного сопротивления образуется резонанс в электрической цепи. Радиолюбители применяют его для настройки на определенную передающую станцию. Конструкторы линий электропередач делают специальные расчеты, чтобы предотвратить броски напряжения и аварийные ситуации. Представленные ниже сведения помогут успешно решать практические задачи на основе особенностей этого явления.

При резонансе в цепи переменного тока резко увеличивается амплитуда сигнала

Причины резонанса

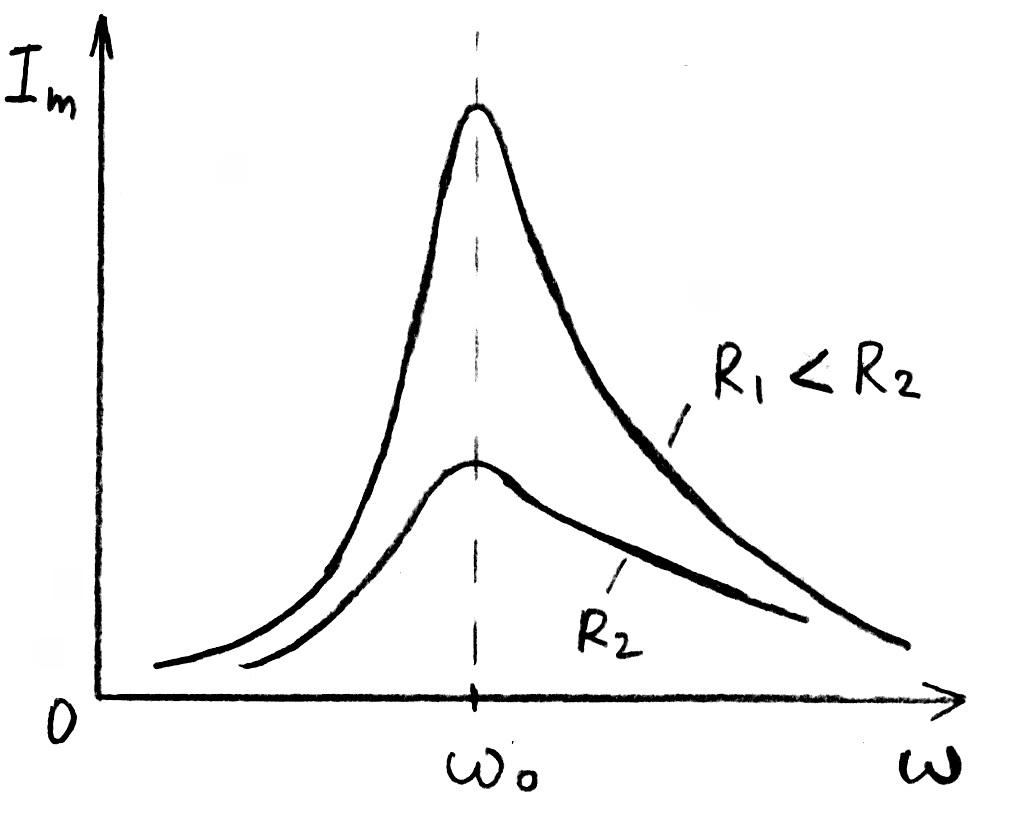
Классический пример с приказом командира идти марширующим солдатам «не в ногу» перед мостом наглядно демонстрирует суть этого явления. Если не использовать такую предосторожность, колебания могут увеличиться до критичного значения, вплоть до разрушения конструкции. Для получения максимальной амплитуды раскачивают в определенном ритме качели. Приведенные примеры демонстрируют существенное увеличение результата при совпадении частот внешнего воздействия и непосредственно самой системы.

Электрический резонанс по своим принципам не отличается от механических аналогов. Он образуется при совпадении частот внешнего сигнала и контура. Функции накопителей энергии выполняют реактивные индукционные и емкостные элементы. Потери (постепенное уменьшение амплитуды) обеспечивает электрическое сопротивление цепи, что аналогично коэффициенту трения.

Принцип резонанса токов

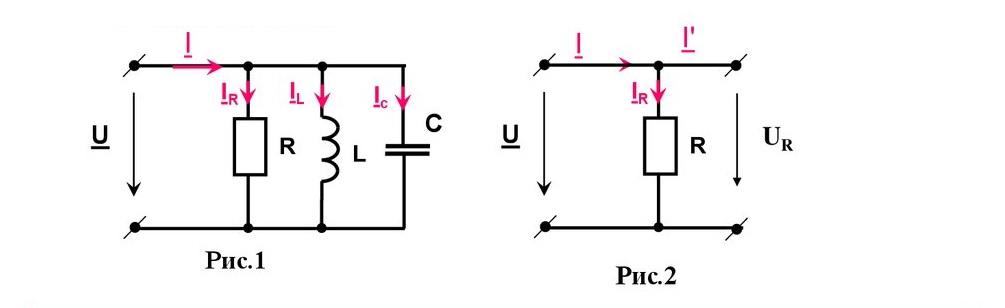
Для создания необходимых условий электро резонанса необходимо создать параллельный контур с тремя типовыми компонентами:

• сопротивлением (R);
• емкостью (C);
• индуктивностью (L).

Схему подключают к источнику питания с напряжением (U)

На определенной частоте суммарные стоки через реактивные элементы (IL, Ic) становятся значительно больше, чем ток источника (I). Это явление называют резонансом тока.

Характеристики резонанса

Это явление образуется при одинаковых реактивных составляющих цепи. Такое распределение позволяет обеспечить равномерную циркуляцию магнитной и электрической составляющих энергии (через индуктивность и конденсатор, соответственно). Такой контур называют «колебательным» по аналогии с механическим маятником.

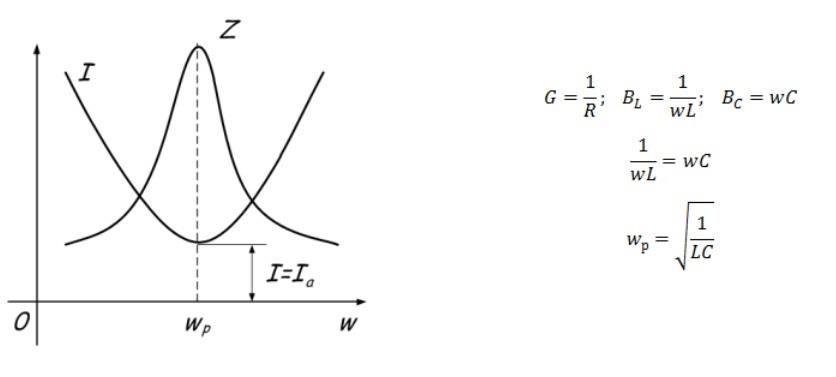
При достижении определенной резонансной частоты (w) в параллельном (последовательном) контуре импеданс максимален (минимален). Соответствующим образом при изменении электрического сопротивления уменьшается (увеличивается) ток.

Резонанс токов и напряжений

Параллельный контур используют, чтобы создать резонанс тока. Для выполнения отмеченных выше условий выбирают равные значения реактивных проводимостей (BL и Bc). По мере увеличения частоты общее сопротивление контура возрастает, что сопровождается уменьшением силы тока.

График изменения тока и проводимости, формулы для расчетов

В последовательном резонансном контуре устанавливают аналогичные функциональные компоненты. Эта схема при достижении резонансной частоты уменьшает сопротивление, что сопровождается существенным увеличением напряжения на реактивных составляющих, по сравнению с электродвижущей силой источника питания.

Резонанс напряжений в цепи переменного тока: график, электрическая схема и формула расчета

RLC-цепь

Для уточнения процессов надо изучить особенности компонентов типовой RLC цепи. Если к источнику переменного тока подсоединить конденсатор, напряжение на его обмотках будет изменяться по аналогии с исходным сигналом. Для расчетов пользуются понятием емкостного сопротивления Xc, которое определяется формулой:

Xc = 1/2π * f * C,

где:

• f – частота;
• С – емкость.

По мере роста частоты увеличивается емкостное сопротивление, и уменьшается ток:

I = U/ Xc.

Этот элемент выполняет определенные ограничительные функции. Однако он не рассеивает энергию c преобразованием в тепло как обычное электрическое сопротивление R.

Для расчета влияния индуктивной составляющей применяют формулы:

• XL = 2π * f * L;
• I = U/XL;
• I = U/2π * f * L.

При подключении катушки к источнику питания образуется магнитное поле, которое препятствует прохождению тока. Формулы демонстрируют прямую зависимость сопротивления от частоты и значения индуктивности (L).

Электрический резонанс

Для полноценного изучения (применения) явления надо учитывать полное сопротивление цепи (Z). Вместе с потерями его можно выразить следующей формулой при последовательном подключении функциональных элементов:

Z = √ R2 + (2π * f * L — 1/2π * f * C)2.

По закону Ома:

I = U/Z = U/  √ R2 + (2π * f * L — 1/2π * f * C)2.

Если соблюдается равенство реактивных составляющих, сопротивление уменьшается с одновременным увеличением силы тока. При соблюдении такого условия несложно вычислить резонансную частоту (Fрез):

• 2π * f * L = 1/2π * f * C;
• Fрез = 1/2π * √ L*C.

Резонанс напряжений, достигающих максимальной амплитуды

Получить наибольшую амплитуду в последовательном контуре можно с помощью изменения следующих параметров:

• индуктивности;
• емкости;
• частоты.

Значения отдельных компонентов устанавливают с применением рассмотренных выше формул. Так, величину емкости можно вычислить следующим образом:

C = 1/ f2 * L.

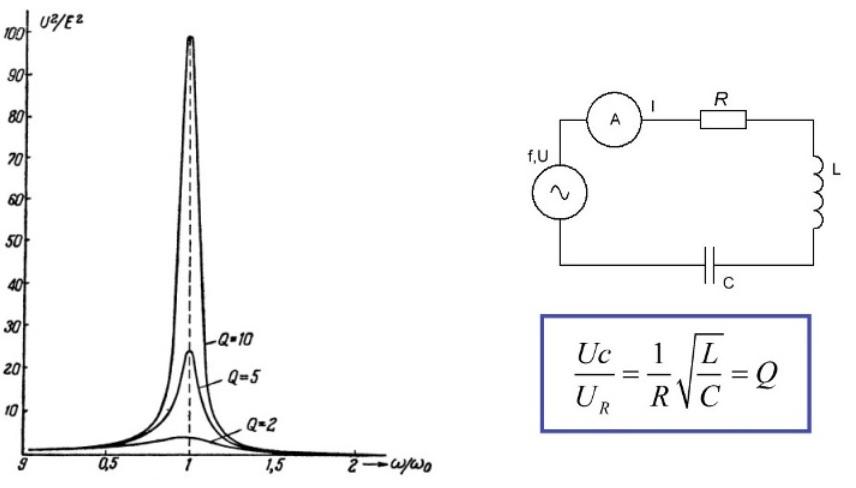
Если реактивные компоненты значительно больше активного сопротивления, на клеммах конденсатора или катушки можно получить повышение напряжения, по сравнению с источником.

Резонанс токов через реактивные элементы

В параллельном контуре оперируют с понятиями реактивных проводимостей (BL и Bc). Как и в предыдущем примере, для создания резонансного режима необходимо обеспечить равенство этих параметров. Дополнительным условием является совпадение частот (источника и контура). Ток при резонансе будет проходить только через активное сопротивление R.

Двойственность RLC-контуров

Из представленных сведений можно сделать два вывода с учетом выбранного варианта соединения функциональных компонентов цепи:

• Последовательный (резонанс напряжений) – минимальное значение импеданса на Fрез, которое в идеальных условиях равно R;
• Параллельный (резонанс токов) – на Fрез импеданс увеличивается до максимального значения.

Собственная частота резонансного контура

Этот параметр вычисляют по формуле:

w = 1/√ L*C.

Если частота контура совпадает с частотой внешнего сигнала, амплитуда колебаний значительно увеличивается.

Применение резонансного явления

Резонанс в электрических цепях используют для фильтрации сигналов. Выбирают соответствующую схему обработки для ограничения необходимого диапазона либо расширения полосы пропускания.

С помощью последовательного контура можно повысить напряжение питания, если снабжающая организация не обеспечивает стабильность параметров сети. Такие неприятности встречаются при подключении потребителей на дачных участках и в коттеджных поселках, в сравнительно небольших населенных пунктах.

Недостаток ликвидируют конденсаторами, которые добавляют в электрическую цепь. Подобные решения помогают восстановить работоспособность дрели, станка, другого мощного оборудования. Обмотки соответствующего привода выполняют функции индуктивного компонента колебательного контура.

Параллельное подключение конденсаторов компенсирует потери, созданные реактивной мощностью. Этот вариант обеспечивает циркуляцию энергии между накопителем и подключенной обмоткой. Без такого дополнения часть энергии будет бесполезно потребляться сетью питания. Следует подчеркнуть, что счетчик в любом случае фиксирует потребление. Данная модернизация поможет сэкономить на оплате коммунальных услуг.

Резонансные явления способны чрезмерно увеличить силу тока или напряжение. Необходим точный расчет электрических цепей, чтобы предотвратить перегрев и повреждение проводов, короткие замыкания и другие аварийные ситуации.

Использование резонанса напряжений для передачи радиосигнала

Применение последовательного колебательного контура удобно изучать на конкретном примере. При конструировании передающих устройств, например, уменьшение импеданса на определенной частоте позволяет сделать настройку на определенный сигнал. Такую задачу решают с помощью колебательного контура.

Распределение спектра на экране измерительного прибора после обработки фильтром

Точно спроектированный фильтр будет «убирать» паразитные составляющие без дополнительных средств контроля и автоматизации. Такое решение, кроме простоты и минимальной стоимости, обеспечивает экономное потребление энергии генератором сигнала.

Как показано на практических примерах, резонанс может выполнять полезные и вредные функции. Точный расчет поможет создать качественную электрическую цепь с заданными техническими параметрами.

Видео

Автор:

Винoгрaдов Aндрeй Aлексaндрoвич