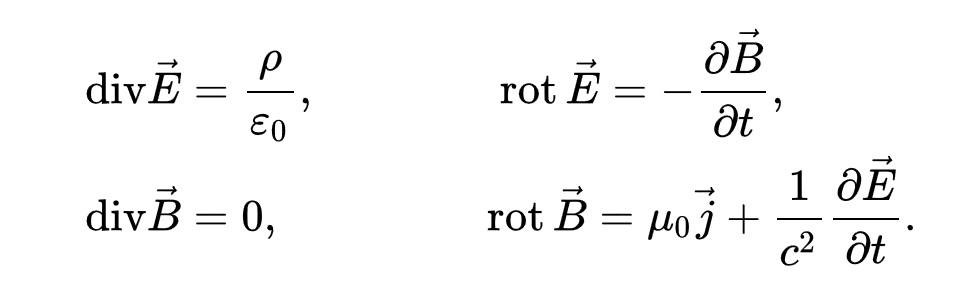Напряженность электрического поля
Содержание
- 1 Напряжённость электрического поля в классической электродинамике
- 2 Как направлен вектор электрического поля
- 3 Сила действия электромагнитного поля на заряженные частицы
- 4 Уравнения Максвелла
- 5 Закон Кулона
- 6 Закон обратных квадратов
- 7 «Материальные уравнения»
- 8 Связь с потенциалами
- 9 Электростатика
- 10 Системы единиц
- 11 Видео
Этим параметром обозначают силовое воздействие на заряд в определенной точке пространства. Напряженность учитывают в процессах распространения радиоволн, при конструировании электродвигателей, для решения других задач. В данной публикации приведены теоретические знания и методики расчетов.
Напряжённость электрического поля в классической электродинамике
Для лучшего понимания темы необходимо напомнить несколько базовых определений. Существуют отрицательные и положительные электрические заряды. Каждый из них не зависит от системы координат, что подразумевает отсутствие влияния скорости. В изолированном объеме сумма зарядов не изменяется. Базовой величиной считают Кулон, который соответствует прохождению тока через единичную площадь сечения проводника за одну секунду.
Электрическое поле:
- создается зарядами;
- распространяется со скоростью света;
- не ограничено в свободном пространстве.
Описывает напряженность электрического поля формула с векторными составляющими:
E=F/q0,
где:
- E – это вектор напряженности, который зависит от координат в пространстве по осям Х, Y, Z и времени;
- F – сила, оказывающая воздействие на единичный точечный заряд q0.
Вместе с вектором магнитной индукции напряженность (Е) формирует электромагнитное поле. Суммарное воздействие сил образует тензор. Вместе с зарядом это главные параметры электродинамики.
Как направлен вектор электрического поля
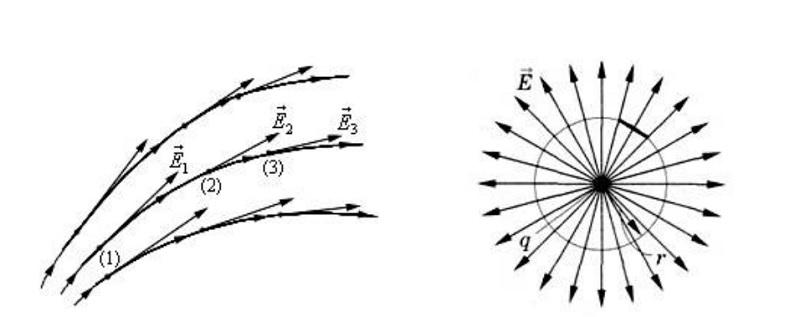
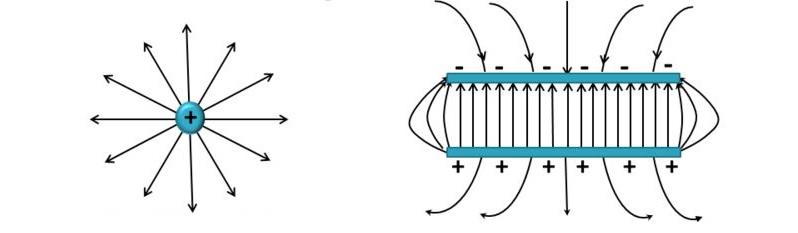
Вектор поля надо направить в сторону от положительного заряда и в обратном направлении – к отрицательному. Это определение справедливо для одной точки. Так как идеальные условия отсутствуют, в реальной ситуации приходится учитывать взаимодействие зарядов и соответствующее образование силовых линий.
Поле не является однородным, что демонстрируют с помощью разных расстояний между отдельными линиями. В примере с пластинами близкое расположение параллельных проводников позволяет обеспечить одинаковую напряженность в рабочей зоне. Все силовые линии бесконечные. Они начинаются на положительном заряде и заканчиваются на отрицательном. Таким образом, направление вектора напряженности будет всегда в сторону уменьшения потенциала.
Сила действия электромагнитного поля на заряженные частицы
Полное силовое воздействие на частицу с учетом магнитной компоненты можно определить с помощью расширенной формулы:
F=Eq0+ q0v * B.
Здесь «*» обозначает умножение векторов скорости (v) заряженной частицы и магнитной индукции (B).
Эта формула напряженности поля предполагает единичный заряд точечного объекта. Вычисленные параметры аппроксимируют на крупные тела с применением соответствующих математических формул.
Уравнения Максвелла
Этими уравнениями описывают трансформацию электрической и магнитной составляющих полей с учетом плотностей тока (j) и заряда (p). Многие типовые задачи вполне можно решить с их помощью. Для исследования взаимного воздействия нескольких систем удобнее пользоваться матричным или интегральным представлением.
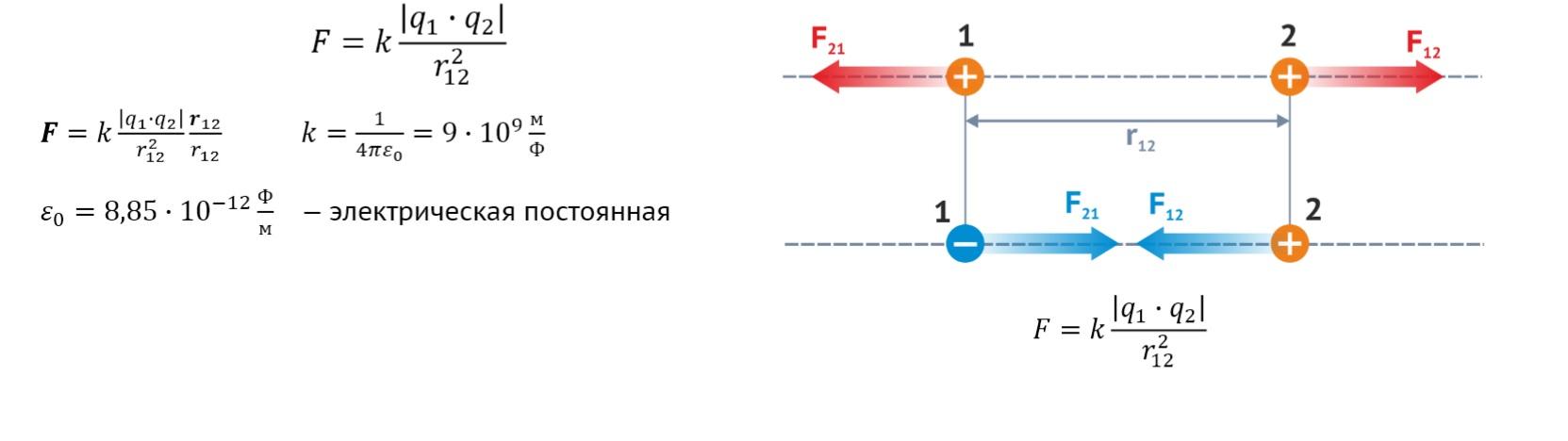
Закон Кулона
С помощью этих формул показано, как найти напряженность при взаимодействии точечных зарядов. Для исключения лишних влияний подразумевается размещение в безвоздушной среде с электрической изоляцией от окружающего пространства. В таких условиях сила будет увеличиваться прямо пропорционально величине зарядов и обратно – квадрату дистанции между данными точками.
Закон обратных квадратов
Это соотношение – производная от рассмотренного выше закона Кулона. В идеальных условиях сила воздействия будет уменьшаться обратно пропорционально квадрату расстояния между зарядами.
«Материальные уравнения»
Для решения многих практических задач вполне достаточна ограниченная точность. С помощью «материальных» уравнений выполняют расчеты различных электрических цепей.
Уместный пример – закон Ома. Он был создан в ходе измерения электрических параметров. В начальном виде формула (Х=П/L+B) состояла из следующих компонентов:
- Х – показания измерительного устройства (гальванометра), включенного в разрыв электрической цепи;
- П – параметры источника питания, заставляющие стрелку прибора отклоняться на определенный угол;
- L – длина соединительных проводов;
- B – общие свойства установки.
Несложно догадаться, что в современном представлении это известный закон, показывающий взаимное влияние основных параметров полной электрической цепи:
I = E/R+r,
где:
- I – ток;
- E – ЭДС (напряжение);
- R и r – сопротивление подключенных компонентов и самого источника питания, соответственно.
Связь с потенциалами
Для отображения этих компонентов удобно пользоваться векторным представлением. Сначала можно выразить работу (А), которую совершает электрическое поле (E) при перемещении заряда (q) на определенное расстояние (L):
A=E*q*L.
Далее ту же величину отображают через разницу потенциалов:
A=q*(ϕ1-ϕ2)=q*U.
Итоговая формула:
E=U/L.
Точнее будет использовать векторное выражение напряженности и передвижения.
Электростатика
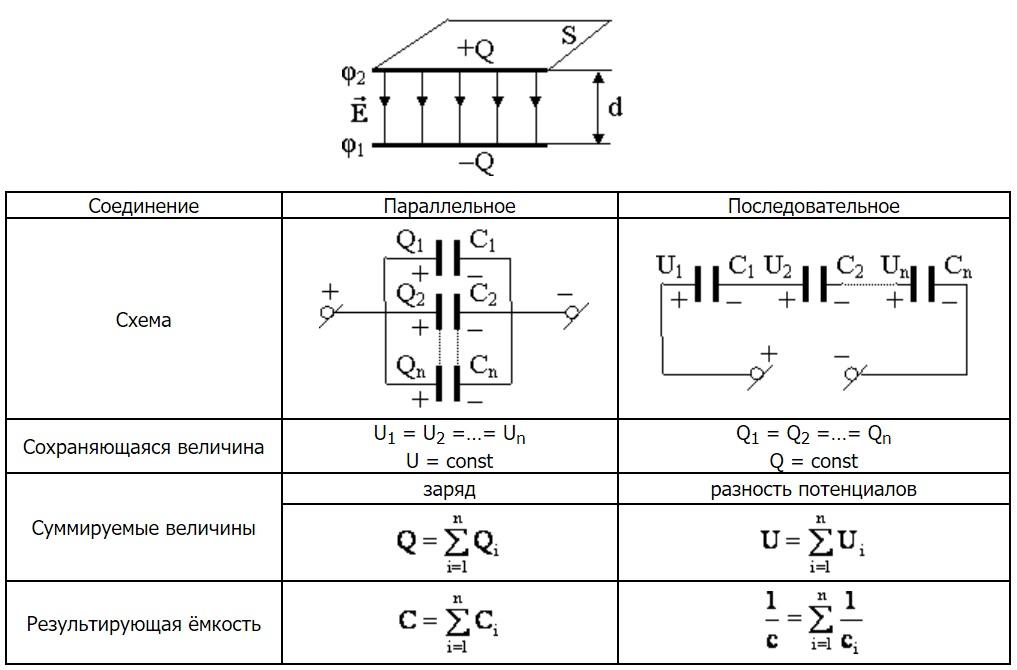
Этот раздел электродинамики описывает частный случай, когда заряженные тела находятся в статичном состоянии. Такая ситуация значительно упрощает расчеты. Для практического примера можно создать электростатический конденсатор.
Устанавливают две плоскости одинаковой размерности параллельно на небольшом расстоянии, разделяют слоем диэлектрика. Если создать разницу потенциалов, между поверхностями образуется поле. В такой конструкции накапливается электрический заряд. Какой будет емкость, можно узнать с помощью этой формулы:
C=Q/ (ϕ1-ϕ2)=Q/U=e*S/d,
где:
- e – проницаемость диэлектрика;
- e0 – электрическая постоянная (8,85*10-12 Ф/м);
- S – площадь пластин;
- D – расстояние между ними.
Чтобы зарядить конденсатор до нужной емкости, надо затратить энергию W=(e*e0*E2/2)*S*D. На рисунке показано, как изменять рабочие параметры сборки при последовательном и параллельном соединении модулей.
Теорема Гаусса
Эта теорема определяет пропорциональность потока вектора напряженности электрического поля (Ф) заряду (Q), который заключен в произвольную поверхность замкнутого типа:
Ф=4π*Q.
Напряжённость электрического поля точечного заряда
В этом случае можно пользоваться рассмотренным выше законом Кулона. В следующих разделах представлены формулы для вычисления в разных системах единиц.
В единицах СИ
В этой системе базовой выбрана сила тока, поэтому кулон является производной величиной.
Основная формула:
F=k*(q1*q2/r122).
Здесь коэффициент k=1/(4π*e0).
Для системы СГС
Здесь, как и в предыдущем примере, выбран единичный заряд – «точка». Основные правила характеризуют физические процессы аналогично. Разница лишь в постоянных величинах. В данном случае коэффициент k обратно пропорционален диэлектрической проницаемости (е) среды.
Напряженность электрического поля произвольного распределения зарядов
В этом варианте для получения результата надо сложить вектора каждого заряда:
Еобщ=Е1+Е2+…+En.
Чтобы обеспечить непрерывность линии напряженности, берут интеграл соответствующей области. Построить распределение силовых линий можно с помощью расчета перемещения вектора по всем точкам.
Системы единиц
Отмеченные ниже различия надо учитывать, чтобы корректно пользоваться формулами, справочными данными. В современной системе СИ напряженность измеряется в вольтах на метр. Однако до сих пор сохраняется альтернативный вариант (СГС), точнее две подсистемы: СГСМ и СГСЭ. Измерять параметры без ошибок помогут следующие данные.
Таблица пересчета напряженности
| Система | Значение | Единицы |
|---|---|---|
| СИ | 1 | Вольт/метр (Ньютон/Кулон) |
| СГСМ | 106 | Абвольт/см |
| СГСЭ | 10^6с^-1 | Статвольт/см |