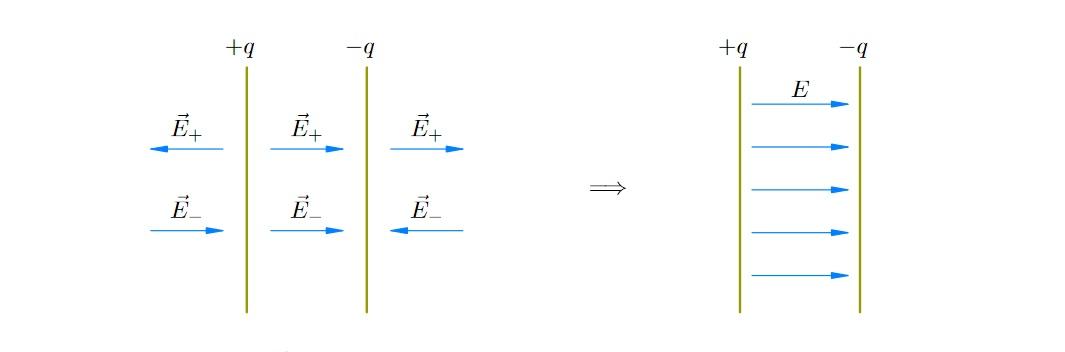Энергия электрического поля
Содержание
Любая частица с электрическим зарядом изменяет свойства окружающего пространства. Аналогичный эффект можно наблюдать при прохождении тока через проводник. Образованное поле характеризуется особым распределением силовых линий. Его энергетические параметры используют для решения различных практических задач.
Современный конденсатор (ионистор) используют для накопления большого количества электроэнергии
Напряженность электрического поля
Энергия поля отличается в разных точках. Для оценки силовых характеристик можно изучить воздействие, которое оказывается на частицы с определенным зарядом (q). В соответствии с базовыми определениями закона Кулона основные зависимости определяются следующим образом:
F (дж) = E *q.
В этой формуле «E» обозначает величину силы, оказывающей π влияние на рассматриваемый заряд в определенной точке пространства. Данный параметр определяет напряженность поля.
Энергия в электростатическом поле
Для объективной оценки силовых параметров изучают воздействия на заряженные тела. Чтобы упростить задачу, можно рассмотреть уединенный проводник, не подверженный внешним влияниям. Для этого случая потенциал (ϕ) будет прямо пропорционален величине заряда (q):
ϕ =q/C, где C – емкость.
Единица измерения – фарад.
При увеличении рабочего элемента следует учесть соответствующие объемные геометрические изменения. Емкость поляризованного шара вычисляют следующим образом:
С = 4π * e0 * R,
где:
- e0 – постоянная = 8,85*10-12 Ф/м, определение электрической проницаемости идеальной среды (вакуума);
- R – радиус.
Как измениться проницаемость в реальных условиях, показывает поправочный коэффициент «e». Соответствующие коррекции можно сделать в представленной формуле:
С = 4π * e0 * e * R.
Научными исследованиями и практическими экспериментами подтверждены следующие особенности:
- вектор напряженности поля направляется в сторону от положительного заряда;
- в реальных условиях приходится учитывать силы взаимодействия зарядов и силовых линий;
- при близком размещении двух пластин с разными зарядами обеспечивается равномерность поля.
Электрическое поле в конденсаторе
На практике не часто применяют емкость уединенных проводников. В реальных условиях приходится учитывать взаимные влияния полей и зарядов. Для решения конкретных задач удобнее использовать конструкции с равномерным распределением силовых линий и выводами для подключения к источнику питания.
Типичный пример такого изделия – плоский конденсатор. Его емкость можно рассчитать по формуле:
C = Q/ (ϕ1-ϕ2) = Q/U = (e * e0 * S)/d,
где:
- ϕ1-ϕ2 – разница потенциалов;
- U – напряжение;
- e – электрическая проницаемость среды (диэлектрика) между пластинами;
- S – площадь рабочих элементов;
- d – расстояние между обкладками.
В этой конструкции специальное расположение рабочих элементов минимизирует воздействие внешней среды. Базовый принцип – площадь пластин (обкладок) должна быть намного больше промежутка между ними. Для упрощения можно подробно изучить конденсатор с воздушным слоем. Для этого случая e = 1, поэтому соответствующий компонент можно устранить из расчетов.
Положительный и отрицательный заряды равны по значениям, но принимаются с разными знаками для обеспечения разницы потенциалов. Напряженность для каждой пластины можно выразить через следующие параметры:
Е+- = P/(2*e0),
где P = q/S – поверхностная плотность, определяющая концентрацию заряда на рабочих обкладках.
Векторное распределение напряженности электрического поля
При векторном представлении несложно понять взаимную компенсацию сил, которые действуют за пределами рабочей зоны:
Евнешн= Е+ — Е- = 0.
Обратная ситуация – между пластинами:
Ераб = Е+ + Е- = P/e0 = q/(S* e0).
Здесь происходит удвоение силовых параметров поля.
В реальных условиях пластины не могут быть бесконечно большими. В некоторых ситуациях приходится учитывать искажения поля за счет «краевых» эффектов. Тем не менее, представленные выше формулы и отношения вполне пригодны для выполнения многих практических расчетов. Существенные коррекции нужно делать при работе с сигналами СВЧ. В типовых сетях (50 Гц) и в границах радиочастотного диапазона соответствующими минимальными искажениями можно пренебречь.
Энергия заряженного конденсатора
Оценить рабочие параметры этого накопительного элемента можно с применением разных методик. Простейший способ – анализ сближения разноименно заряженных пластин. Это перемещение обеспечивает сила (F), прямо пропорциональная величине заряда (q) и напряженности (E):
F = q * E.
Добавив E = q/(2*e0*S), получают формулу физики для оценки взаимодействия:
F = q2/(2*e0*S).
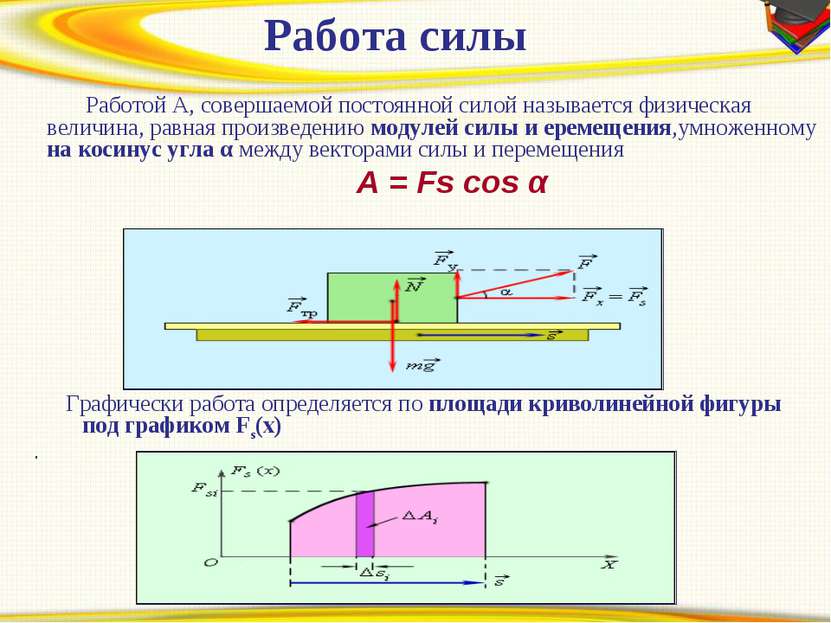
Так как работа (A) равна произведению силы (F) на пройденное расстояние (d – дистанция между пластинами), энергия электрического поля конденсатора вычисляется без большого труда:
W = A = F * d = d *q2/(2*e0*S).
С учетом емкости C = d /(e0*S) после элементарных математических преобразований можно получить итоговую формулу:
- W = q2/(2*C);
- q = C * U;
- W = ½ (C * U2).
Емкий конденсатор обеспечивает функционирование источника света без подключения к сети
Объемная плотность электрической энергии
Рассмотренные выше зависимости и формулы можно преобразовать, чтобы уточнить влияние связанных параметров на энергетический потенциал определенной конструкции:
- W = ½ (C * U2) = d *q2/(2*e0*S) = ((e0 * E2)/2) * S*d;
- однако произведение S*d равно объему (V);
- таким образом, исходное выражение для расчета приобретает вид:
W = ((e0 * E2)/2) * V.
По итоговому варианту становится понятным, сколько энергии электрического поля сосредоточено внутри определенного объема. Исходя из того можно сделать вывод о наличии соответствующих свойств самого поля. Теоретические знания подтверждены расчетами. Для оценки эффективности конкретных изделий применяют удельный показатель (объемную плотность) w = W/V = (e0 * E2)/2. При заполнении диэлектриком формулы дополняют соответствующими данными электрической проницаемости (e).
Вектора магнитной индукции (В) и напряженности (Е) формируют электромагнитное поле. Для расчета силы, перемещающей соленоид, надо учитывать силовые компоненты в совокупности. Соответствующие коррекции делают при создании колебательного контура. Максимальный энергетический потенциал можно получить с помощью увеличения диэлектрической проницаемости слоя между обкладками конденсатора.
